Mind mapping is a diagram in which you can
demonstrate concepts, ideas, or words and link
them together. It is a great technique to brainstorm
idea without having everything in structure. It is
based around a central topic allowing sub-topics,
without having to use a linear layout. Some benefits
of mind mapping are flexibility, boosts creativity,
and is a great way to put down your thoughts.
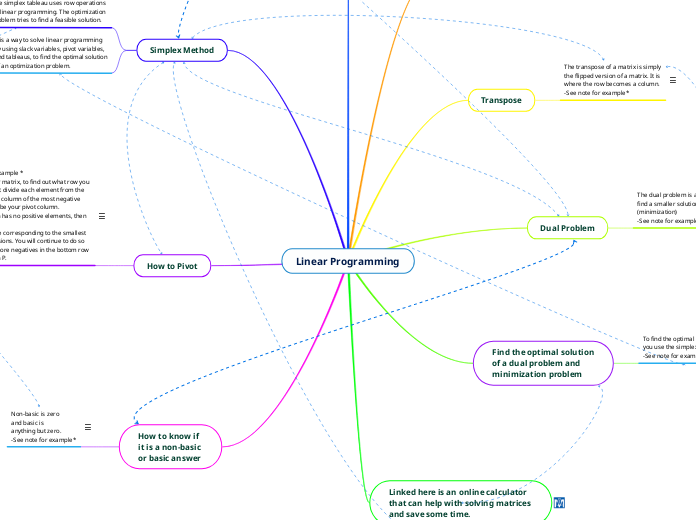
The transpose of a matrix is simply
the flipped version of a matrix. It is
where the row becomes a column.
-See note for example*
Example if, 1 3 2 A= 5 7 4when we transpose A, it becomes 1 5A= 3 7 2 4
The dual problem is a way to
find a smaller solution,
(minimization)
-See note for example*
Min. C= 4x1 + 2x2Subject to 2x1 + 5x2 _> 7 x1 + 7x2 _> 6To form the Dual Problem, you will write the equation above in a matrix and transpose. Max. P= 7y1 + 6y2Subject to 2y1 + y2 _> 4 5y1 + 7y2 _> 2Using the slack variables x1 and x2 write the initial system and simplex tableau for the dual problem.2y1 + y2 + x1 = 45y1 + 7y2 + x2 =2-7y1 + -6y2 + P = 0Simplex tableau: 2 1 1 0 0 4 5 7 0 1 0 2-7 -6 0 0 1 0
To find the optimal solution
you use the simplex method.
-See note for example*
If we are given the following: Min. C= 20x1 + 32x2 Subject to 3x1 + 2x2 _> 10 6x1 + 7x2 _> 19 Max. P= 10y1 + 19y2Subject to 3y1 + 6y2 <_ 20 2y1 + 7y2 <_ 32y1 y2 x1 x2 P1 2 0.33 0 0 6.670 3 -0.67 1 0 18.670 1 3.33 0 1 66.67The optimal solution of the dual problem is Max. P= 66.67 y1= 6.67 y2= 0The optimal solution of minimization problem isMin. C= 66.67 x2= 18.67
A mathematical technique where a
linear function can be maximized or
minimized when subjected to various
constraints. The solution is to find the
optimal value of the linear equation.
The simplex tableau uses row operations
on linear programming. The optimization
problem tries to find a feasible solution.
It is a way to solve linear programming
by using slack variables, pivot variables,
and tableaus, to find the optimal solution
of an optimization problem.
-Look at Note for example *
Once you have your matrix, to find out what row you
will be using to pivot divide each element from the
last column and the column of the most negative
indicator, which will be your pivot column.
*If the pivot column has no positive elements, then
there is no solution.
The pivot row will be corresponding to the smallest
result from the divisions. You will continue to do so
until there are no more negatives in the bottom row
to the left of column P.
x1 x2 x3 s1 s2 P 1 3 2 1 0 0 850 850/2 =4252 1 1 0 1 0 500 500/1 =500-5 -7 -10 0 0 1 0 As indicated above we see the pivot point in column x3 because -10 is the most negative number in our bottom row and row 1 becuase it gives us the smallest result.
Non-basic is zero
and basic is
anything but zero.
-See note for example*
Solve the following matrix and find the solution for P, x1, and x3. Know if they are non-basic or basic solutions.x1 x2 x3 s1 s2 P 1 3 2 1 0 0 850 850/2 =4252 1 1 0 1 0 500 500/1 =500-5 -7 -10 0 0 1 0 Once the matrix has been solved, the columns that only show zeros and 1 are your basic solutions, in whichever row the 1 is in that will be your answer. The other colums will be non-basic solutions.x1 x2 x3 s1 s2 P 0.5 1.5 1 0.5 0 0 425 1.5 -0.5 0 -0.5 1 0 75 0 8 0 5 0 1 4250 The basic solutions are:P= 4250x3= 425 s2= 75The non-basic solutions are:x1= 0x2= 0 s1= 0