Matrices
Una matriz es un conjunto de números ordenados en filas y columnas.
Las matrices tienen por nombre una letra mayúscula y sus elementos se encierran entre dos paréntesis (o dos corchetes)
Book title

Decimos que una matriz es de orden m x n o de dimencion mxn cuando tiene m filas y n columnas
Propiedades de las matrices
Propiedad 1.
El determinante del producto de matrices es el producto de sus determinantes
Propiedad 2.
El determinante de una matriz con alguna fila o columna de ceros es 0.
Propiedad 3.
Se puede extraer factor común de una fila o columna multiplicando el determinante por el factor
Propiedad 4.
Se puede extraer el mismo factor común de n
filas o columnas multiplicando el determinante por el factor elevado a n
Propiedad 5.
Si se cambia el orden de una fila o de una columna, el determinante cambia de signo.
Propiedad 6.
Si se cambia el orden de n
filas o columnas, el determinante cambia de signo si n
es impar.
Propiedad 7.
Si una matriz es invertible, el determinante de la inversa es el inverso del determinante:
Propiedad 8.
El determinante de una matriz es igual al de su traspuesta:
Propiedad 9.
Si una matriz tiene filas o columnas linealmente dependientes, entonces su determinante es 0
Propiedad 10.
El determinante no cambia si se suman filas (o columnas) multiplicadas por números distintos de 0.
Propiedad 11.
El determinante de una matriz diagonal es el producto de los elementos de su diagonal.
Propiedad 12.
El determinante de una matriz triangular es el producto de los elementos de su diagonal
Tipo de las matrices
Matriz fila
Una matriz fila está constituida por una sola fila. La matriz rectangular tiene distinto número de filas que de columnas, siendo su dimensión mxn
Matriz columna
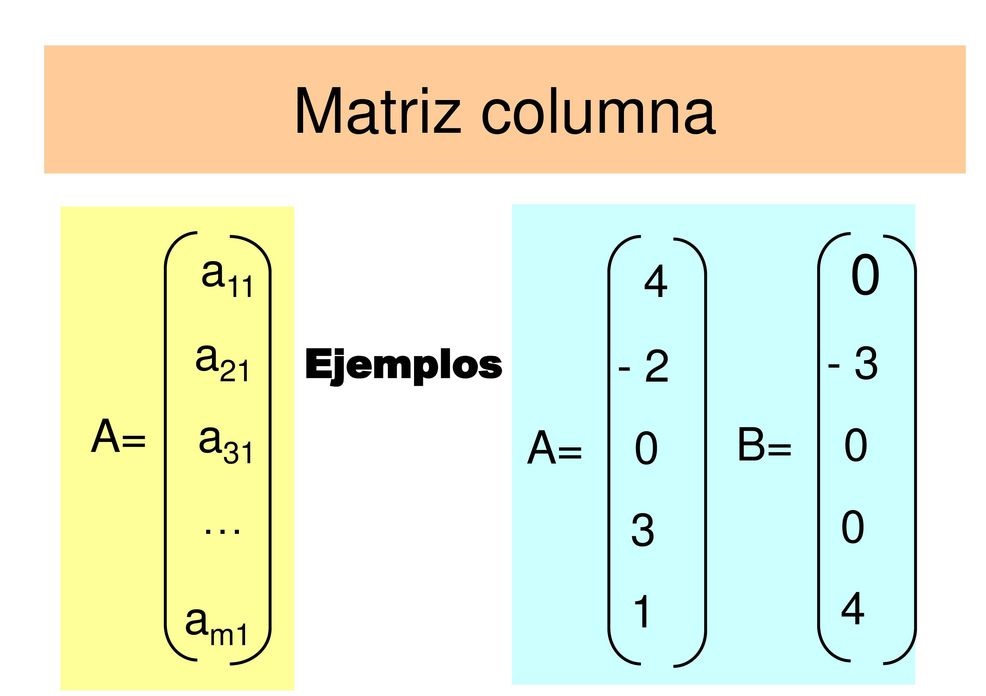
Podemos pensar los vectores como casos particulares de matrices:
Matriz nula
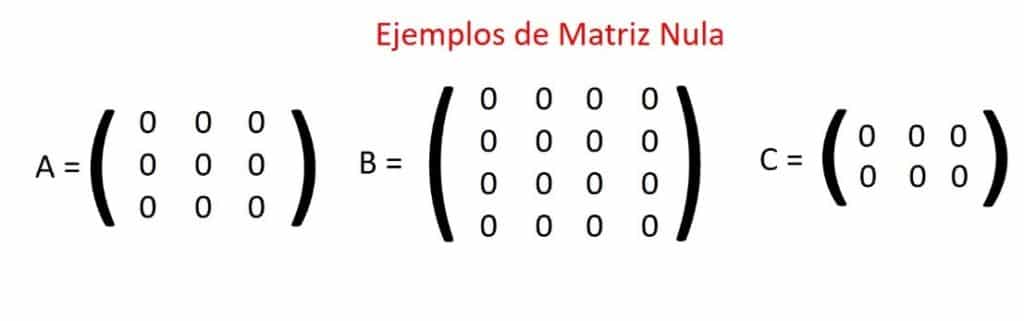
La matriz nula (o matriz cero) es una matriz la cual todos sus elementos son igual a cero (0).
Igualdad de matrices

Para que dos matrices se consideren iguales deben tener el mismo número de elementos y, además, los elementos deben ocupar la misma posición en ambas matrices.