Real Numbers
Euclid's Division Lemma
1) According to this, given positive
integers a and b , there exist unique
integers q and r satisfying
a= bq+r, 0 <= r <b
Euclid's Division Algorithm
Euclid's deivision algorithm is a technique
to compute HCF (Highest Common Factor)
of 2 given integers.
Eg. Suppose we need to find the HCF of
455 and 42, therefore by Euclid's Division
Algorithm,
Since 455 > 42,
455 = 42 x 10 + 35
=> 42 = 35 x 1 +7
=> 35 = 7 x 5 + 0
Therefore, HCF is the divisor, i.e, 7.
1) Euclid's division lemma
and algorithm are so
closely interlinked that
people even call the prior
one as the Division algorithm also.
2) Although the Euclid's Division
Algorithm is only for positive integers,
it can be extended for all integers except 0 i.e.,
b is not equal to 0.
3) Let there be 2 numbers a and b
therefore, a x b = HCF(a,b) x LCM(a,b)
Some other Theorems
1. Let p be a prime number. If p divides a2, then p divides a, where
a is a positive integer.
2. Let x be a rational number whose decimal expansion terminates.
Then x can be expressed in the form ,
p/q where p and q are coprime,
and the prime factorisation of q is of the form 2n5m, where n, m are non-negative integers.
3. Let x = p/q be a rational number, such that the prime factorisation of q is of the form 2n5m, where n, m are non-negative integers. Then x has a decimal expansion which terminates.
4. Let x =
p/q, where p and q are coprimes, be a rational number,
such that the prime factorisation of q is not of the form 2n5m, where n, m are
non-negative integers. Then, x has a decimal expansion which is non-terminating repeating (recurring).
Methods of factorisation
1)Long division method
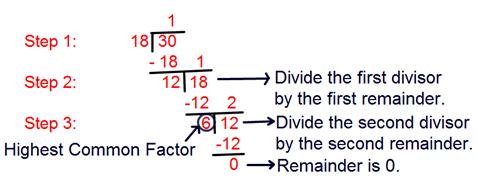
2) Factor Tree
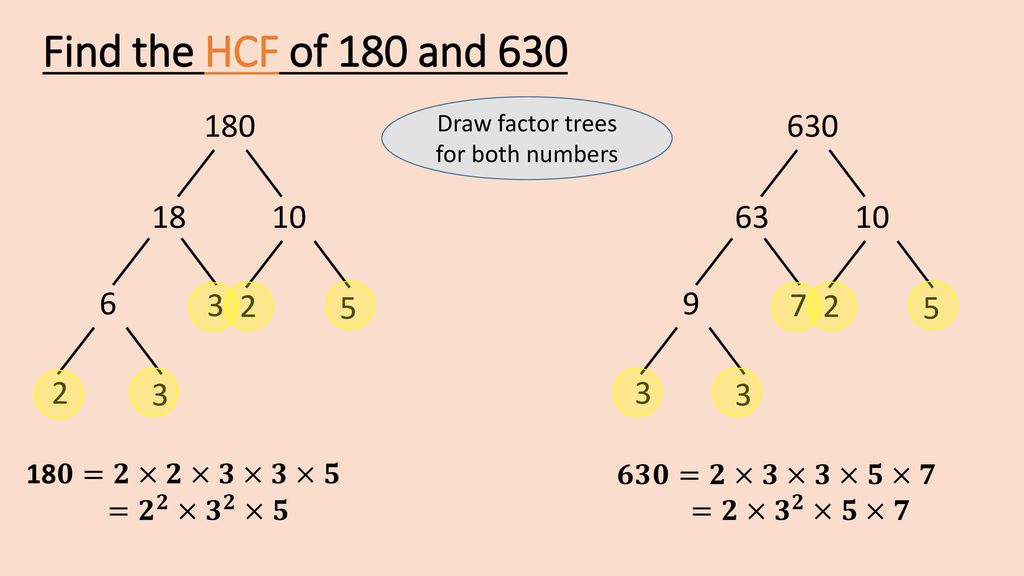
3) Prime Factorisation

The Fundamental Theorem of Arithmetic
Every composite number can be expressed as a product of primes and this factorisation is unique apart from the order in the which those primes occur.