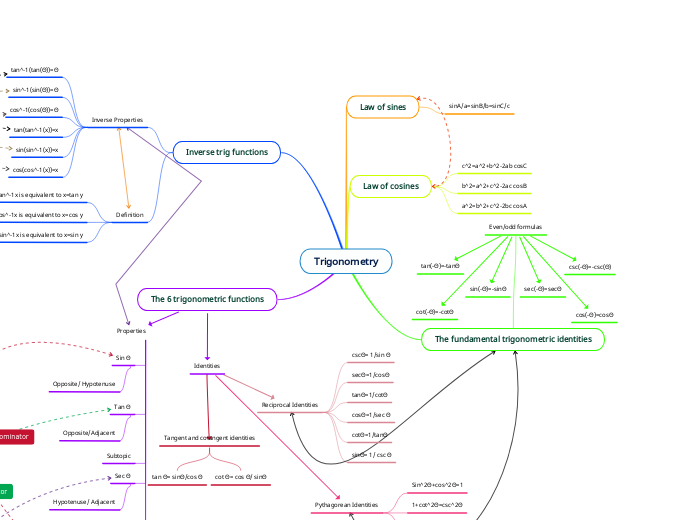
sinA/a=sinB/b=sinC/c
c^2=a^2+b^2-2ab cosC
b^2=a^2+c^2-2ac cosB
a^2=b^2+c^2-2bc cosA
Even/odd formulas
sin(-Θ)=-sinΘ
csc(-Θ)=-csc(Θ)
cot(-Θ)=-cotΘ
sec(-Θ)=secΘ
tan(-Θ)=-tanΘ
cos(-Θ)=cosΘ
Inverse Properties
tan^-1(tan(Θ))=Θ
sin^-1(sin(Θ))=Θ
cos^-1(cos(Θ))=Θ
tan(tan^-1(x))=x
sin(sin^-1(x))=x
cos(cos^-1(x))=x
Definition
y=tan^-1x is equivalent to x=tan y
y=cos^-1x is equivalent to x=cos y
y=sin^-1x is equivalent to x=sin y
Properties
Sin Θ
Opposite/ Hypotenuse
Tan Θ
Opposite/Adjacent
Subtopic
Sec Θ
Hypotenuse/ Adjacent
Cot Θ
Adjacent/ Opposite
Csc Θ
Hypotenuse/ Opposite
Cos Θ
Adjacent/ Hypotenuse
Identities
Tangent and cotangent identities
tan Θ= sinΘ/cos Θ
cot Θ= cos Θ/ sinΘ
Reciprocal Identities
cscΘ= 1/sin Θ
secΘ=1/cosΘ
tanΘ=1/cotΘ
cosΘ=1/sec Θ
cotΘ=1/tanΘ
sinΘ= 1/ csc Θ
Pythagorean Identities
Sin^2Θ+cos^2Θ=1
1+cot^2Θ=csc^2Θ
tan^2Θ+1=sec^2Θ