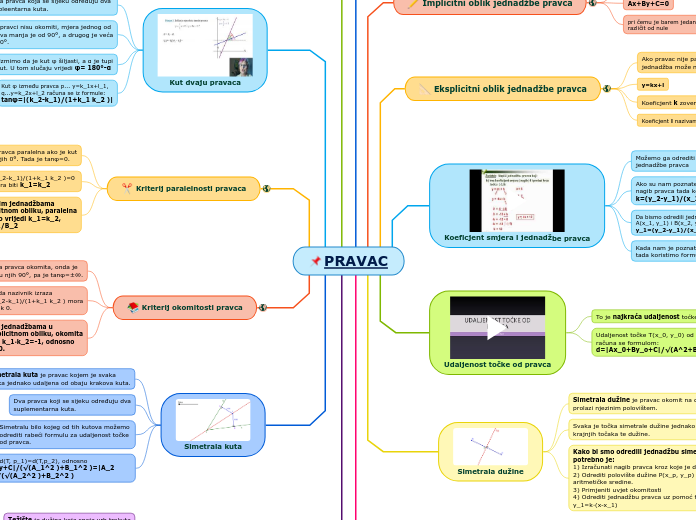
PRAVAC
Segementni oblik jednadžbe pravca
Ako su (m, 0) i (0, n) točke u kojima pravac siječe
koordinatne osi onda pravac ima jednadžbu:
x/m+y/n=1
Slovom x označava se odsječak što ga pravac čini
sa koordinatnim osima. Zbog toga vrijedi formula x^2=m^2+n^2
Iz slike možemo zaključiti da se radi o pravokutnom trokutu, radi toga površina trokuta se računa po formuli:
P=|m ∙n|/2
Implicitni oblik jednadžbe pravca
Pravac je skup svih točaka (x,y) u ravnini
čije koordinate zadovoljavaju jednadžbu:
Ax+By+C=0
pri čemu je barem jedan od koeficjenta A, B
različit od nule
Eksplicitni oblik jednadžbe pravca
Ako pravac nije paralelan s osi ordinta, njegova se jednadžba može napisati u obliku
y=kx+l
Koeficjent k zovemo nagib ili koeficjent smjera
Koeficjent l nazivamo odsječak na osi ordinata.
Koeficjent smjera i jednadžbe pravca
Možemo ga odrediti uz pomoć eksplicitnog oblika jednadžbe pravca
Ako su nam poznate kordinate točaka i trebamo odrediti nagib pravca tada koristimo formulu:
k=(y_2-y_1)/(x_2-x_1 )
Da bismo odredili jednadžbu pravca koji prolazi točkama A(x_1, y_1) i B(x_2, y_2) tada koristimo sljedeću formulu: y-y_1=(y_2-y_1)/(x_2-x_1 )∙(x-x_1)
Kada nam je poznat koeficjent smjera i točka T(x_1,x_2), tada koristimo formulu: y-y_1=k∙(x-x_1)
Udaljenost točke od pravca
To je najkraća udaljenost toćke T i neke točke prvca p.
Udaljenost točke T(x_0, y_0) od pravca p...Ax+By+C=0 računa se formulom:
d=|Ax_0+By_o+C|/√(A^2+B^2 )
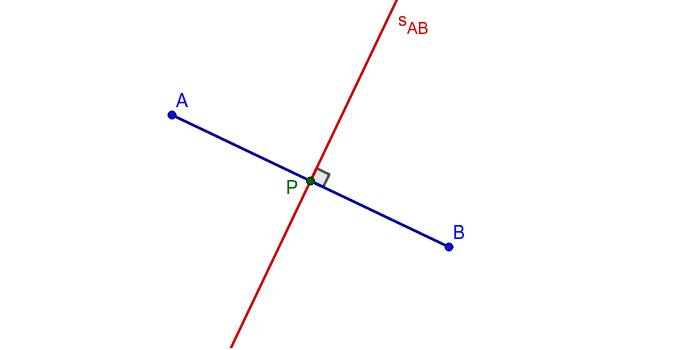
Simetrala dužine
Simetrala dužine je pravac okomit na dužinu koji prolazi njezinim polovištem.
Svaka je točka simetrale dužine jednako udaljena od
krajnjih točaka te dužine.
Kako bi smo odredili jednadžbu simetrale dužine potrebno je:
1) Izračunati nagib pravca kroz koje je dužina određena
2) Odrediti polovište dužine P(x_p, y_p) preko aritmetičke sredine.
3) Primjeniti uvjet okomitosti
4) Odrediti jednadžbu pravca uz pomoć formule: y-y_1=k∙(x-x_1)

Ortocentar
Pravci koji sadrže visine trokuta sijeku se
u jednoj točki koja se naziva ortocentar.
Da bi došli do koordinata ortocentra potrebno je:
1) Zadovoljiti uvjet okomitosti prema koefic+jentu smjera za
visine i stranie trokuta
2)Odrediti jednadžbe pravca za visine trokuta
3)Moramo izjednačiti dvije jednadžbe visina kako bi smo dobili jednadžbu sa dvije nepoznanice i koordinate ortocentra
Pravci paralelni s koordinatnim osima
Jednadžbu By+C=0 zadovoljavaju sve točke
(x, y) ravnine za koje vrijedi y= -C/B. Te se
točke nalaze na pravcu koji prolazi točkom
(0,-C/B) i paralelan je s osi apscisa.
Jednadžbu Ax+C=0 zadovoljavaju sve točke
(x, y) ravnine za koje vrijedi y= -C/A. Te se
točke nalaze na pravcu koji prolazi točkom
(-C/A, 0) i paralelan je s osi ordinata.
Kut dvaju pravaca
Dva pravca koja se sijeku određuju dva
supleentarna kuta.
Ako pravci nisu okomiti, mjera jednog od
kutova manja je od 90°, a drugog je veća
od 90°.
Uzmimo da je kut φ šiljasti, a α je tupi
kut. U tom slučaju vrijedi φ= 180°-α
Kut φ između pravca p... y=k_1x+l_1,
q...y=k_2x+l_2 računa se iz formule:
tanφ=|(k_2-k_1)/(1+k_1 k_2 )|
Kriterij paralelnosti pravaca
Dva su pravca paralelna ako je kut
između njih 0°. Tada je tanφ=0.
Iz formule (k_2-k_1)/(1+k_1 k_2 )=0
vidimo da mora biti k_1=k_2
Dva pravca zadana svojim jednadžbama
u eksplicitnom ili implicitnom obliku, paralelna
su onda i samo onda ako vrijedi k_1=k_2,
odnosno A_1/A_2 =B_1/B_2
Kriterij okomitosti pravca
Ako su dva pravca okomita, onda je
kut između njih 90°, pa je tanφ=±∞.
To znači da nazivnik izraza
tanφ=(k_2-k_1)/(1+k_1 k_2 ) mora
biti jednak 0.
Dva pravca zadana jednadžbama u
eksplicitnom ili implicitnom obliku, okomita
su onda ako vrijedi k_1∙k_2=-1, odnosno
A_1A_2+B_1B_2=0.
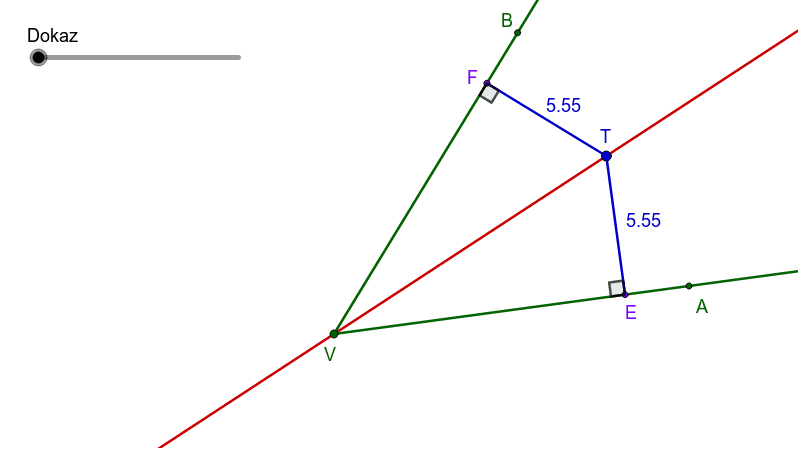
Simetrala kuta
Simetrala kuta je pravac kojem je svaka
točka jednako udaljena od obaju krakova kuta.
Dva pravca koji se sijeku određuju dva
suplementarna kuta.
Simetralu bilo kojeg od tih kutova možemo
odrediti rabeći formulu za udaljenost točke
od pravca.
To znači da je d(T, p_1)=d(T,p_2), odnosno
|A_1 x+B_1 y+C|/(√(A_1^2 )+B_1^2 )=|A_2 x+B_2 y+C|/(√(A_2^2 )+B_2^2 )
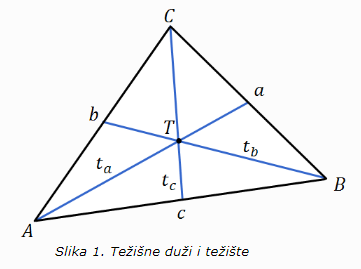
Težište i težišnica
Težište je dužina koja spaja vrh trokuta
i polovište nasuprotne stranice.
Sve tri težišnice trokuta sjeku se u jednoj
točci koju nazivamo težišnicom.
Kako bi smo odredili jednadžbu težišta i težišnicu,
potrebno je:
1) Odrediti polovište dužine P(x_p, y_p) preko aritmetičke sredine.
2)Koristiti formulu y-y_1=(y_2-y_1)/(x_2-x_1 )∙(x-x_1) da bi odredili težište određene dužine.
3)Moramo izjednačiti dvije jednadžbe težišnice kako bi smo dobili jednadžbu sa dvije nepoznanice i koordinate težišnice