numeros reales
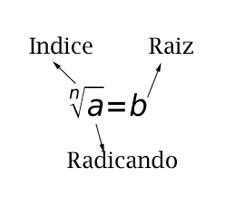
raices enesimas
se denomina raiz enesima de un n° real "a", al n° "b" que satisfase
racionales
números naturales
números enteros
son los que se pueden expresar de la forma
a/b

irracionales
es aquel que posee una representación decimal finita no periodica


propiedades
potencia de una raiz enesima

raiz enesima de una raiz enesima

producto de raices de igual indice

cociente de una raiz enesima

b^n=a
potencias
propiedades
a^p . a^q = a^p+q
a^p : a^q = a^p-q
a^p . b^p = (a . b)^p
a^p : b^p = (a : b)^p
(a^p)^q = a^p.q
logaritmo
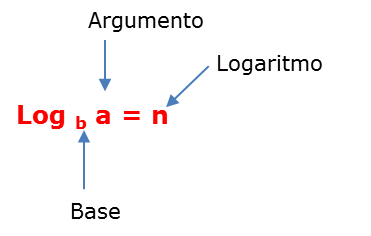
logaritmo en base b de argumento a
caracteristicas
base no puede ser (-), ni 0 ni 1
argumento siempre (+)
log b^a
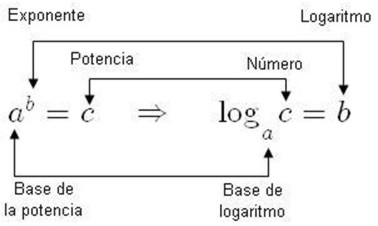
expresion que establece una equivalencioa entre log y potencia

racionalizacion
se le llama racionalización al proceso de obtener fracciones equivalentes pero que no tenga raíces en el denominador