Trigonometri

Teori består af : Definitioner, (Illustrationer), Sætninger og Beviser.SPØRGSMÅL 2 : Hvad har man IKKE brug for, når man regner opgaver? 

Generelt er definitioner (præcise) forklaringer af nye begreber.SPØRGSMÅL 3 : Hvilke definitioner har I lært i trigonometri?

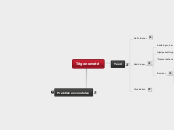
Sætninger kan (groft sagt) opdeles i tre kategorier.  SPØRGSMÅL 4 : Hvilke tre kategorier er der tale om? (Se mind-mappen)Dette er dog min (ganske uofficielle) inddeling.SPØRGSMÅL 5 : Hvilke sætninger/regler har man brug for ved beregning i vilkårlige trekanter?

Sætninger/regler, der direkte sigter på "praktisk" anvendelse eller brug i opgaver.SPØRGSMÅL 8: Hvilke regler handler det om ved beregning i vilkårlige trekanter?

Sætninger, der ikke i sig selv er beregnet på praktisk brug, men som er beregnet på at hjælpe med at bevise anden teori.SPØRGSMÅL 9 : Hvilke regler drejer det sig om ved beregning i vilkårlige trekanter?

Faget på gymnasiet er en slags mini-udgave af det videnskabelige fag matematik, og "præsentationsteori" er teori, der er tradition for at man "skal kunne" - men som I måske ikke kan se den dybere mening med.SPØRGSMÅL 10 : Hvilke regler drejer det sig om ved beregning i vilkårlige trekanter?(Svaret skulle helst ikke blive "det hele" :) )

Ingen regler/sætninger må bruges, uden at reglen er bevist/forklaret.Enkelte steder her i gymnasiet er vi nødt til at "snyde", fordi et (korrekt) bevis ikke lader sig gøre indenfor gymnasiepensum. 

Hvis man vil bevise en regel/sætning, skal man have nogle forudsætninger, eksempelvisandre regler/sætninger, eller måske en figur. SPØRGSMÅL 11 : Vi har bevist cosinus-relationen.  Hvad var forudsætningerne?

Argumentationen i et bevis er en forklaring på, hvordan man (via logiske argumenter) kommer fra forudsætninger til konklusion.Denne forklaring skal i princippet være umulig at modsige, men på gymnasieniveau "snyder" vi af og til, og nøjes med et argument, der virker "nogenlunde sandsynligt".SPØRGSMÅL 12 : Hvad er vores argumenter, når vi vil bevise cosinus-relationen? (kort forklaring)

Den bedste argumentation er et stringent matematisk bevis, der 100% sikkert beviser reglen/sætningen.SPØRGSMÅL 14 : ER vore beviser for cosinus-relation, sinus-relation og areal strengt stringente beviser?(Men her på gymnasie-niveau kan det ikke altid lade sig gøre).

Konklusionen er selve sætningen.SPØRGSMÅL 13 : Hvad kunne det være?

SPØRGSMÅL 6 : Hvorfor skal man (helst) lave en illustration, inden man begynder at regne en opgave?

Praktisk anvendelse vil ofte her i gymnasiet være opgaver, der skal løses ved hjælp af den (forhåbentligt) kendte teori. SPØRGSMÅL 1 : Hvor har I haft brug for formler for retvinklede trekanter, cosinus-relationen, sinus-relationen, arealformlen?