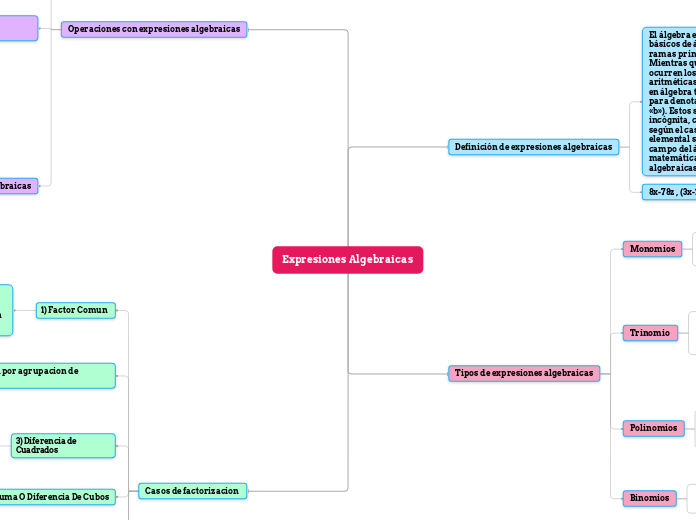
Expresiones Algebraicas
Definición de expresiones algebraicas
El álgebra elemental incluye los conceptos básicos de álgebra, que es una de las ramas principales de las matemáticas. Mientras que en la aritmética solo ocurren los números y sus operaciones aritméticas elementales (como +, –, ×, ÷), en álgebra también se utilizan símbolos para denotar números (como «x», «y», «a», «b»). Estos se denominan variables, incógnita, coeficientes, índices o raíz, según el caso. El término álgebra elemental se usa para distinguir este campo del álgebra abstracta, la parte de la matemática que estudia las estructuras algebraicas.
8x-78z , (3x-1)/(9x-2), 3 naranjas + 4 papas.
Tipos de expresiones algebraicas
Monomios
Un monomio es una expresión algebraica formada por un solo término.
-2x2 ; 3x ; -5x3 ; x5 son cuatro monomios de grados 2, 1, 3 y 5 respectivamente.
Trinomio
un trinomio es una expresión algebraicas de únicamente tres monomios, sumados o restados.
5, 2 y 4 son las constantes (números enteros), mientras que p, r y s son las variables del trinomio.
Polinomios
es una expresión algebraica formada por la suma de varios monomios o términos, cada uno de los cuales es el producto de un coeficiente constante y de valor conocido.
3x+2x-5
Binomios
un binomio consta únicamente de una suma o resta de dos monomios.
a+b
Operaciones con expresiones algebraicas
Suma y resta de expresiones algebraicas
primero agrupamos los términos semejantes, es decir, aquellos que tienen la misma variable y exponente. Luego, sumamos los coeficientes de los términos
la resta es encontrar la cantidad desconocida que, cuando se suma al sustraendo (el elemento que indica cuánto hay que restar), da como resultado el minuendo (el elemento que disminuye en la operación).
Multiplicación de expresiones algebraicas
Para multiplicar dos monomios se aplica la regla de los signos, se multiplican los coeficientes y para las literales iguales se escribe la literal y se suman los exponentes, si las literales son diferentes se pone cada literal con su correspondiente exponente.
Se multiplica cada monomio del primer polinomio por todos los elementos segundo polinomio. Se suman los monomios del mismo grado. Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.
División de expresiones algebraicas
Para dividir un monomio entre un monomio, divide los coeficientes (o simplifícalos como lo harías con una fracción) y divide las variables con bases iguales restando sus exponentes.
Cuando dividimos un polinomio por un número, el resultado es otro polinomio que cumple las siguientes características : El polinomio resultante es del mismo grado que el polinomio que fue dividido. Sus coeficientes resultan de dividir cada uno de los coeficientes del polinomio entre el número.
Casos de factorizacion
1) Factor Comun
EJEMPLO: 5∙8 + 5∙9
2) Factor comun por agrupacion de terminos.
El factor común por agrupación de términos es un procedimiento algebraico que permite escribir algunas expresiones algebraicas en forma de factores, cuando no todos los términos poseen algo en común.
EJEMPLO: 4a(3) - 1 - a(2) -4a
Una diferencia de cuadrados es el resultado del producto de dos binomios conjugados: Esto implica que, para factorizar una diferencia de cuadrados, se extraen las raíces cuadradas de los términos y se forma un binomio.
EJEMPLO: x²-25 puede factorizarse como (x+5)(x-5).
4) Suma O Diferencia De Cubos
La suma de cubos, es la suma de dos números o variables elevadas al cubo.
EJEMPLO: 8x(3) + 64
5) Trinomio Cuadrado perfecto
Un trinomio cuadrado perfecto es un polinomio de tres términos que cumple con las siguientes características: El primer y tercer término tienen raíces cuadradas exactas. El segundo término es el resultado de multiplicar esas dos raíces por dos.
EJEMPLO: (x + 3)2 = (x + 3)(x + 3) = x2 + 6x + 9. El trinomio x2 + 6x + 9 es un trinomio cuadrado perfecto.
6) Trinomio de la forma x(2)+bx+c
pueden factorizarse encontrando dos enteros, r y s, cuya suma sea b y cuya resta sea c.
EJEMPLO: x(2) + 7x+ 10 = (x + 5) (x +2)
7) Trinomio de la forma ax(2)+bx+c
Para factorizar un trinomio de la forma ax2 + bx + c, encuentra los enteros, r y s, cuya suma sea b y cuyo producto sea ac. Reescribe el trinomio como ax2 + rx + sx + c y luego agrupa y aplica la propiedad distributiva para factorizar el polinomio.
EJEMPLO: 6x² -7x -3