Geometric
Sequence and Series

Series

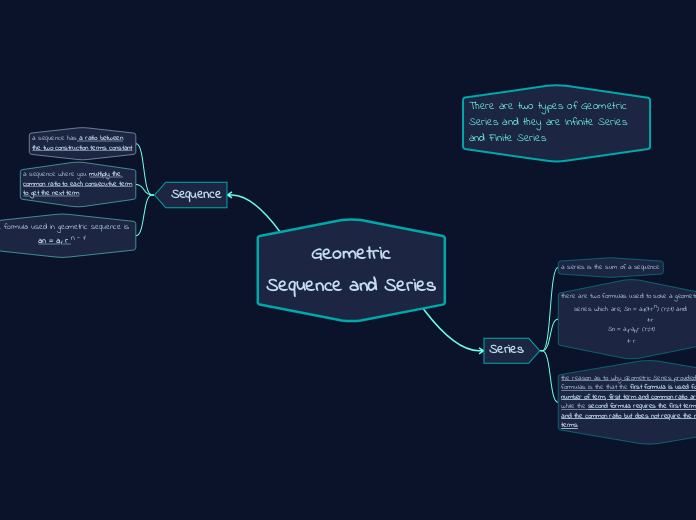
a series is the sum of a sequence

there are two formulas used to solve a geometric
series which are; Sn = a1(1−rn) (r≠1) and
1-r
Sn = a1−anr (r≠1)
1− r

n = number of terms

a1 = first term

r = common ratio

an = last term

the reason as to why Geometric Series provided two
formulas is the that the first formula is used for when the
number of term, first term and common ratio are known,
while the second formula requires the first term, last term
and the common ratio but does not require the number of the terms

Sequence

a sequence has a ratio between
the two construction terms constant

a sequence where you multiply the
common ratio to each consecutive term
to get the next term

the formula used in geometric sequence is
an = a1 r n - 1

n = nth term

a1 = first term

r = common ratio

The difference between Geometric Sequence and Geometric Series is the fact that a Geometric sequence is a list of numbers with a ratio between two consecutive terms.
While a Geometric series is the sum of a geometric sequence.

There are two types of Geometric Series and they are Infinite Series and Finite Series