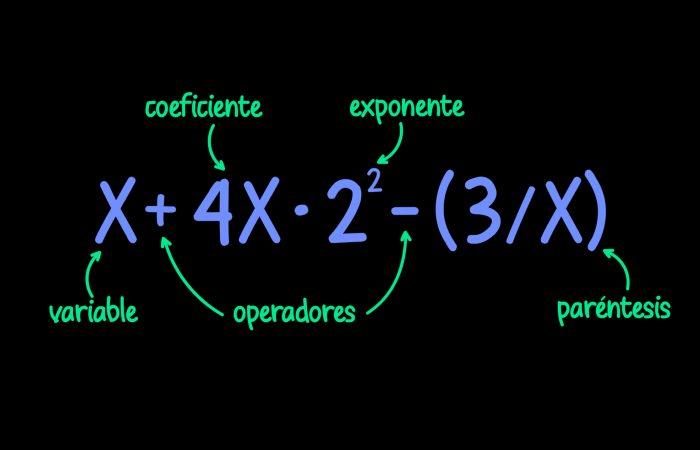
Expresiones algebraicas
¿Qué son?

Una expresión algebraica es una combinación de letras y números ligadas por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación. Las expresiones algebraicas nos permiten, por ejemplo, hallar áreas y volúmenes.
¿Qué significa (termino) dentro de ellas?
Un término es una expresión algebraica fundamental en la que sólo existen operaciones de multiplicación y división de números y letras. El número se llama coeficiente y las letras forman la parte literal. Tanto el número como la letra pueden recibir un poder especial. Estos se dividen con los signos suma y resta en una expresión algebraica con múltiples significados.
Tipos de terminos
Termino independiente
El término independiente, es el que consta de solo un valor numérico y no tiene parte literal.
Termino semejante
Semejantes términos tienen la misma parte literal (con las mismas letras elevadas a los mismos exponentes) y diferencian solo en el coeficiente. Solo se pueden sumar y restar términos similares. Los términos que no son sinónimos no se pueden sumar ni restar; sin embargo, cualquier tipo de término se puede multiplicar o dividir. Si hay muchos términs relacionados en una expresión algebraica, pueden simplificarse sumándolos o restándolos.
Tipos de Expresiones de algebraicas
Existen estos tipos

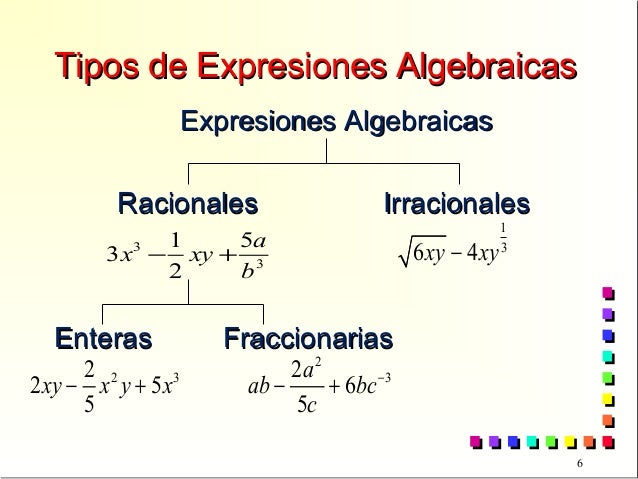
Irracionales
Son aquellos en los que una o más de sus variables se ve afectada por radicales o fraccionarios.

Racionales
Son aquellas en que las variables están afectadas únicamente por las operaciones de suma, resta, multiplicación y división, y en caso de haber potencias, están van estar afectadas únicamente con exponentes enteros.

Racionales enteras
Una Racional Entera Expresión es una en la que sus variables son relacionadas con las operaciones de suma, resta, multiplicación, y división, y si existen potencias, estas son de exponentes naturales.

Racionales fraccionarias
Una expresión Racional Fraccionaria (No Entera) es aquella en la que una o más de las variables forman parte de un divisor o aparecen en un numerador con un exponente negativo.
Clasificación según el numero de términos
Binomio
es una combinación de dos elementos matemáticos (llamados miembros), en el marco de una ecuación o de una relación entre cantidades o estructuras.

Ejemplos binomio al cuadrado
Trinomio
es una expresión algebraica que tiene tres términos.

Ejemplo trinomio cuadrado perfecto
Cuatrimonio
es una expresión algebraica un polinomio formado por cuatro términos
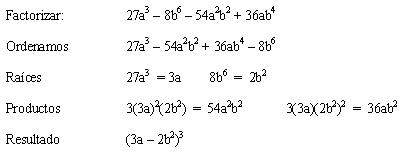
Ejemplo cuatrimonio cubo perfecto
Tipos de expresiones algebraicas

Monomio
Es aquel consta de un solo término o en que los términos que la forman están relacionados por la operación producto.

Polinomio
En él se interrogan varios números y letras, con cantidades, multiplicidades y / o potencias utilizadas para enlazarlos. Las variables se escriben con letras porque pueden tomar varios valores, mientras que los números se denominan coeficientes.

Suma
Para realizar la suma de dos o más polinomios, se debe sumar los coeficientes de los términos cuya parte literal sean iguales, es decir, las variables y exponentes (o grados) deben ser los mismos en los términos a sumar.
Metodo
Pasos:
1 Ordenar los polinomios del término de mayor grado al de menor.
2 Agrupar los monomios del mismo grado.
3 Sumar los monomios semejantes.
Ejemplo del primer método para sumar polinomios
Sumar los polinomios P(x) = 2x³ + 5x − 3, Q(x) = 4x − 3x² + 2x³.
1. Ordenamos los polinomios, si no lo están.
P(x) = 2x³ + 5x − 3
Q(x) = 2x³ − 3x² + 4x
2.Agrupamos los monomios del mismo grado.
P(x) + Q(x) = (2x³ + 5x − 3) + (2x³ − 3x² + 4x)
P(x) + Q(x) = (2x³ + 2x³) + (− 3 x²) + (5x + 4x) + (− 3)
3.Sumamos los monomios semejantes.
P(x) + Q(x) = 4x³ − 3x² + 9x − 3

Resta
Consiste en sumar al minuendo el opuesto del sustraendo. También podemos restar polinomios escribiendo el opuesto de uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.
Metodo
Ejemplo de resta de polinomios
1.Restar los polinomios P(x) = 2x3 + 5x - 3, Q(x) = 2x³ - 3x² + 4x.
P(x) − Q(x) = (2x³ + 5x − 3) − (2x³ − 3x² + 4x)
2.Obtenemos el opuesto al sustraendo de Q(x).
P(x) − Q(x) = 2x³ + 5x − 3 − 2x³ + 3x² − 4x
3.Agrupamos.
P(x) − Q(x) = 2x³ − 2x³ + 3x² + 5x − 4x − 3
4.Resultado de la resta.
P(x) − Q(x) = 3x² + x − 3

Multiplicación
se obtiene multiplicando cada término del primero por el segundo y reduciendo luego los términos semejantes. De este modo obtenemos el polinomio resultante. Así, comprobamos así como nos da la misma solución por ambos métodos.
Metodo
Los coeficientes del polinomio que resulta, son el producto de los coeficientes del polinomio inicial, por el número y dejando las mismas partes literales.
Ejemplos:
13 · (2x³ − 3x² + 4x − 2) = 6x³ − 9x² + 12x − 6
22(3x³ + 4x² + 2x − 1) = 6x³ + 8x² + 4x − 2
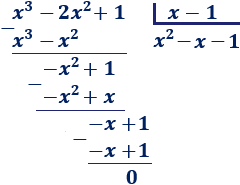
División
En la división de un polinomio por un monomio se divide cada uno de los monomios que forman el polinomio por el monomio, hasta que el grado del dividendo sea menor que el grado del divisor.
Metodo
Explicación con el ejemplo
Resolver la división de los polinomios P(x) = x5 + 2x3 − x − 8, Q(x) = x2 − 2x + 1.
P(x) : Q(x)
1.A la izquierda situamos el dividendo. Si el polinomio no es completo dejamos huecos en los lugares que correspondan.
Ejemplo división de polinomios
2.A la derecha situamos el divisor dentro de una caja.
3.Dividimos el primer monomio del dividendo entre el primer monomio del divisor.
x5 : x2 = x3
4.Multiplicamos cada término del polinomio divisor por el resultado anterior y lo restamos del polinomio dividendo:

5.Volvemos a dividir el primer monomio del dividendo entre el primer monomio del divisor. Y el resultado lo multiplicamos por el divisor y lo restamos al dividendo.

6.Procedemos igual que antes.

7Como en los pasos anteriores, dividimos 8x^2 por x^2, y obtenemos 8.
Multiplicamos por 8 cada término del divisor y obtenemos:
8x^2 - 16x + 8
Procedemos con la resta:
(8x^2 - 6x - 8)-(8x^2 - 16x +8)= 8x^2 - 6x - 8 + 8x^2 + 16x - 8 = 10x - 16
10x − 16 es el resto, porque su grado es menor que el del divisor y por tanto no se puede continuar dividiendo.
x3+2x2 +5x+8 es el cociente.