METODO SIMPLEX

INTRODUCCIÓN

es un método analítico de solución de problemas de programación lineal capaz de resolver modelos mas complejos que los resueltos mediante el método grafico, sin restricción en el numero de variables.

consiste en recorrer los vértices de un poliedro de manera que aumente o disminuya el valor de la función objetivo (según sea el contexto, maximizar o minimizar).

HISTORIA

fue creado en el año de 1947 por el estadounidense George Bernard Dantzig y el ruso Leonid Vitalievich Kantorovich.

ANÁLISIS D POST-OPTIMALIDAD

Analisis Sensibilidad

Nos permite determinar cuales son aquellos parámetros para los que nuestra solución es sensible a cambios y que requieren exactitud al momento de calcularlos y monitoreo constante durante la implementación de la solución.

En PL Los parámetros (datos de entrada) del método pueden cambiar dentro de ciertas límite sin que cambie la solución óptima

El análisis de sensibilidad gráfica para determinar las condiciones que mantendrán la optimalidad de la solución de una PL de 2 variables

Precios Sombra

Nos permite saber el nuevo valor de la función objetivo
a raíz del aumento o disminución de mis recursos, o mas bien de los lados derechos de mis restricciones.

Re-optimizacion

La ventaja de aplicar la Re-optimización es que frecuentemente la solución básica inicial del nuevo modelo solo requiere pocas iteraciones para encontrar la nueva la solución óptima.

PASOS DEL METODO SIMPLEX

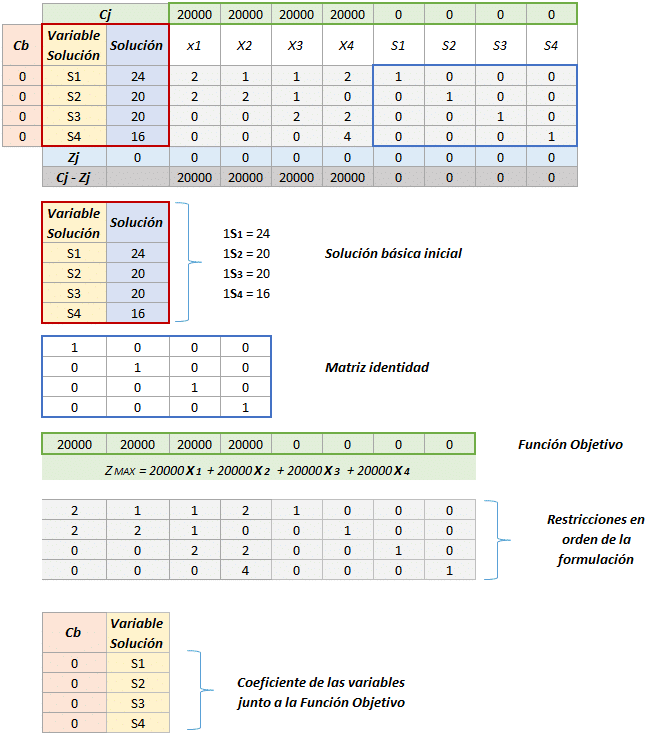
Paso 1. Determinar una solución básica factible de inicio.
Paso 2. Seleccionar una variable de entrada aplicando la condición de optimalidad. Detenerse si no hay variable de entrada; la última solución es la óptima.
Paso 3. Seleccionar una variable de salida aplicando la condición de factibilidad.

Paso 4. Determinar la nueva solución básica con los cálculos adecuados de Gauss-Jordan. Ir al paso 2.

FRONTERAS DE RESTRICCION

es una recta
que marca el límite de lo que permite la
restricción correspondiente.

VENTAJAS

Permite eliminar una base inicial infactible en el caso de restricciones del tipo = ó ≥, sin necesidad de introducir variables artificiales.

Presenta ventajas en algunos casos de análisis de sensibilidad, como la adición de nuevas restricciones o nuevas variables

Topic principal

Algoritmo en modelos de maximización

Soluciones básicas factibles

Método símplex primal-dual

Tabla primal-dual

Método para modelos con combinación
de desigualdades

Algoritmo símplex-dual

TIPOS DE OBTIMIZACION

MAXIMIZACION

DONDE EL VALOR OBTIMO ES MAYOR

MINIMIZACION

DONDE EL VALOR OBTIMO ES MENOR

Subtopic