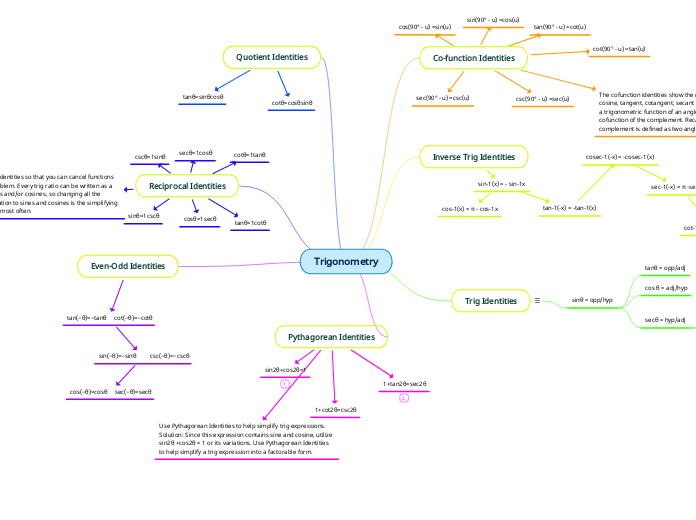
sec(90° - u) =csc(u)
csc(90° - u) =sec(u)
sin(90° - u) =cos(u)
tan(90° - u) =cot(u)
cos(90° - u) =sin(u)
cot(90° - u) =tan(u)
The cofunction identities show the relationship between sine, cosine, tangent, cotangent, secant and cosecant. The value of a trigonometric function of an angle equals the value of the cofunction of the complement. Recall from geometry that a complement is defined as two angles whose sum is 90°.
sin-1(x) = - sin-1x
cos-1(x) = π - cos-1x
tan-1(-x) = -tan-1(x)
cosec-1(-x) = -cosec-1(x)
sec-1(-x) = π -sec-1(x)
cot-1(-x) = π – cot-1(x)
b h
sinθ = opp/hyp
tanθ = opp/adj
cos θ = adj/hyp
secθ = hyp/adj
cotθ = adj/opp
cscθ = hyp/opp
tanθ=sinθcosθ
cotθ=cosθsinθ
sinθ=1cscθ
cosθ=1secθ
tanθ=1cotθ
secθ=1cosθ
cscθ=1sinθ
cotθ=1tanθ
You use reciprocal identities so that you can cancel functions and simplify the problem. Every trig ratio can be written as a combination of sines and/or cosines, so changing all the functions in an equation to sines and cosines is the simplifying strategy that works most often.
tan(−θ)=−tanθ cot(−θ)=−cotθ
sin(−θ)=−sinθ csc(−θ)=−cscθ
cos(−θ)=cosθ sec(−θ)=secθ
sin2θ+cos2θ=1
1+tan2θ=sec2θ
1+cot2θ=csc2θ
Use Pythagorean Identities to help simplify trig expressions. Solution: Since this expression contains sine and cosine, utilize sin2θ +cos2θ = 1 or its variations. Use Pythagorean Identities to help simplify a trig expression into a factorable form.