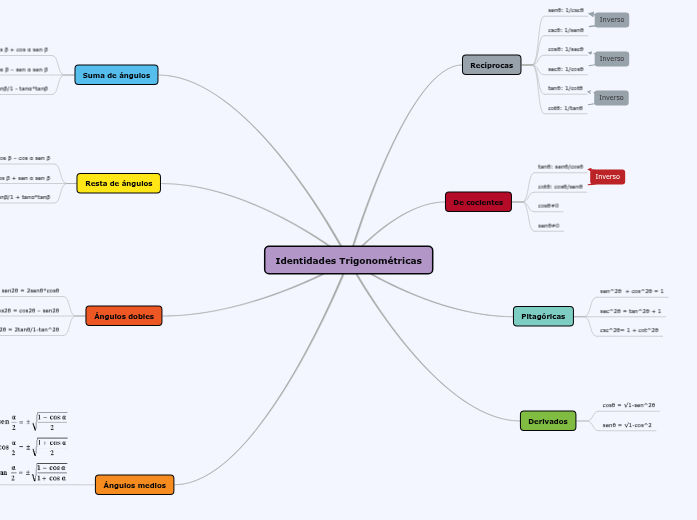
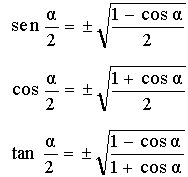Identidades Trigonométricas
Recíprocas
senθ: 1/cscθ
cscθ: 1/senθ
cosθ: 1/secθ
secθ: 1/cosθ
tanθ: 1/cotθ
cotθ: 1/tanθ
De cocientes
tanθ: senθ/cosθ
cotθ: cosθ/senθ
cosθ≠0
senθ≠0
Pitagóricas
sen^2θ + cos^2θ = 1
sec^2θ = tan^2θ + 1
csc^2θ= 1 + cot^2θ
Derivados
cosθ = √1-sen^2θ
senθ = √1-cos^2
Suma de ángulos
sen (α + β) = sen α cos β + cos α sen β
cos (α + β) = cos α cos β – sen α sen β
tan(α + β) = tanα + tanβ/1 - tanα*tanβ
Resta de ángulos
sen (α – β) = sen α cos β – cos α sen β
cos (α – β) = cos α cos β + sen α sen β
tan(α - β) = tanα - tanβ/1 + tanα*tanβ
Ángulos dobles
sen2θ = 2senθ*cosθ
cos2θ = cos2θ – sen2θ
tan2θ = 2tanθ/1-tan^2θ
Ángulos medios