Didáctica de la Matemática II

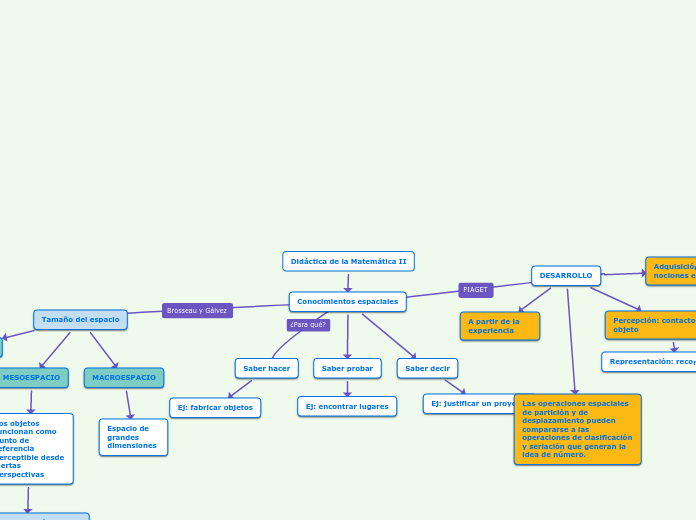
Conocimientos espaciales

Saber hacer

Ej: fabricar objetos

Saber probar

Ej: encontrar lugares

Saber decir

Ej: justificar un proyecto

DESARROLLO

A partir de la experiencia

Percepción: contacto con el objeto

Representación: recordar objetos

Adquisición temprana de nociones espaciales

logra distinguir entre figuras cerradas y abiertas, diferenciar el espacio interior del exterior a una frontera dada o determinar posiciones relativas al interior de un orden lineal.

Las operaciones espaciales de partición y de desplazamiento pueden compararse a las operaciones de clasificación y seriación que generan la idea de número.

Tamaño del espacio

MICROESPACIO

Próxima al sujeto. Accesible a la manipulación y a la visión.

Ejemplo de situación: Delante del alumno se disponen pilas de 20 cajas de fósforos perforadas y al lado se dispone otra
caja llena de fósforos. Hay que poner un fósforo y sólo uno dentro de cada caja

MESOESPACIO

Los objetos funcionan como punto de referencia perceptible desde ciertas perspectivas

Ejemplo de situación: Se dispone de 18 casilleros ubicados en 3 hileras superpuestas de 6 casilleros cada una, con un largo
total de 2,50 m. Esto juega el papel de un conjunto de buzones que el alumno debe llenar con sólo una carta por buzón . Las cartas están en una caja colocada sobre un banco al costado de los casilleros

MACROESPACIO

Espacio de grandes dimensiones