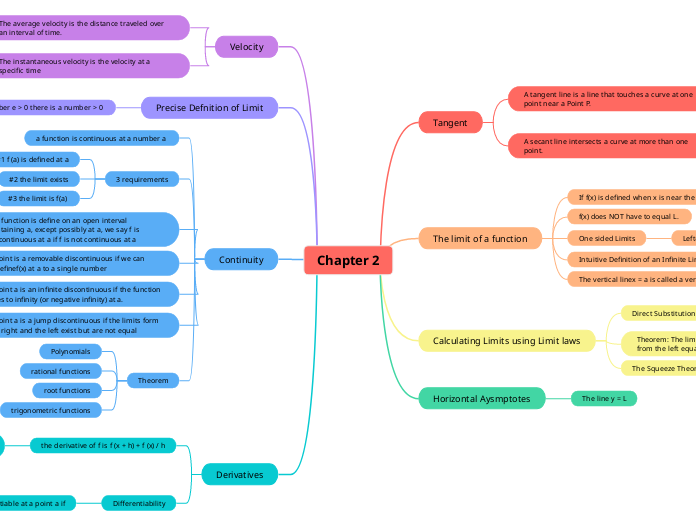
Chapter 2
Tangent
A tangent line is a line that touches a curve at one point near a Point P.
A secant line intersects a curve at more than one point.
Equation of a line
Ax+By = C
y = mx+b
Point Slope Form
y-y1 = m (x-x1)
y - f (x1) = m (x-x1)
The limit of a function
If f(x) is defined when x is near the number.
f(x) does NOT have to equal L.
One sided Limits
Left-hand limit of f(x) as x approaches a
Intuitive Definition of an Infinite Limit
The vertical linex = a is called a vertical asymptote
Calculating Limits using Limit laws
Direct Substitution Property
If f is a polynomial or rational function and a is in the domain of f the limit function = f (a)
Theorem: The limit exists if and only if the limit from the left equals the limit from the right
The Squeeze Theorem
Horizontal Aysmptotes
The line y = L
Velocity
The average velocity is the distance traveled over an interval of time.
s (t) = change in position / change in time
The instantaneous velocity is the velocity at a specific time
"velocity"
limit
Precise Defnition of Limit
if for every number e > 0 there is a number > 0
Continuity
a function is continuous at a number a
3 requirements
#1 f (a) is defined at a
#2 the limit exists
#3 the limit is f(a)
if a function is define on an open interval containing a, except possibly at a, we say f is discontinuous at a if f is not continuous at a
A point is a removable discontinuous if we can redefinef(x) at a to a single number
A point a is an infinite discontinuous if the function goes to infinity (or negative infinity) at a.
f (a) may or may not
A point a is a jump discontinuous if the limits form the right and the left exist but are not equal
Theorem
Polynomials
rational functions
root functions
trigonometric functions
Derivatives
the derivative of f is f (x + h) + f (x) / h
provided the limit exists and a is in the doamin of f . If f' (x) exists, we say f is differentable at a.
If f is differentiable on every point of an interval I, we say that f is differentiable on I
Differentiability
a function will fail to be differentiable at a point a if
1. There is a cusp or "kink" at a
The function is discontinuous at a
There is a vertical tangent at a
The function does not exist at a