POLYNOMIALS
f(x) = a1 + a1x + a1 x²....... a1x²

THOREMS

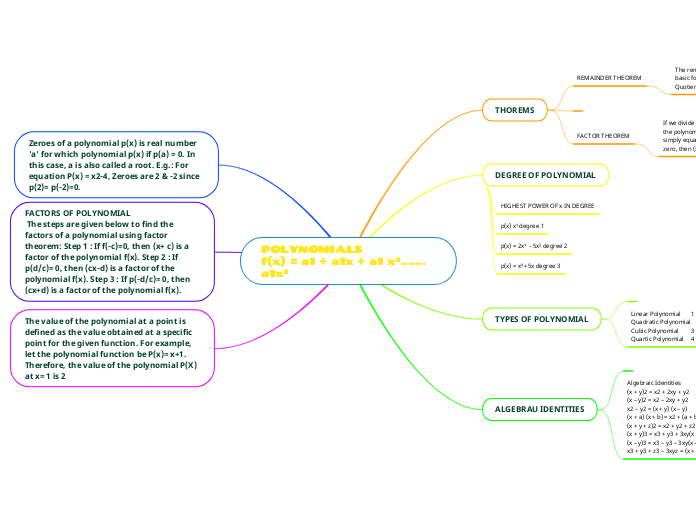
REMAINDER THEOREM

The remainder theorem formula is: p(x) = (x-c)·q(x) + r(x). The basic formula to check the division is: Dividend = (Divisor × Quotient) + Remainder.

FACTOR THEOREM

If we divide a polynomial f(x) by (x - c), and (x - c) is a factor of the polynomial f(x), then the remainder of that division is simply equal to 0. ... If the remainder of such a division is not zero, then (x - c) is not a factor.

DEGREE OF POLYNOMIAL

HIGHEST POWER OF x IN DEGREE

p(x) x¹ degree 1

p(x) = 2x¹ - 5x² degree 2

p(x) = x³ +5x degree 3

TYPES OF POLYNOMIAL

Linear Polynomial 1 3x+1
Quadratic Polynomial 2 4x2+1x+1
Cubic Polynomial 3 6x3+4x3+3x+1
Quartic Polynomial 4 6x4+3x3+3x2+2x+1

ALGEBRAU IDENTITIES

Algebraic Identities
(x + y)2 = x2 + 2xy + y2
(x – y)2 = x2 – 2xy + y2
x2 – y2 = (x + y) (x – y)
(x + a) (x + b) = x2 + (a + b)x + ab.
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx.
(x + y)3 = x3 + y3 + 3xy(x + y)
(x – y)3 = x3 – y3 – 3xy(x – y)
x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)

Zeroes of a polynomial p(x) is real number 'a' for which polynomial p(x) if p(a) = 0. In this case, a is also called a root. E.g.: For equation P(x) = x2-4, Zeroes are 2 & -2 since p(2)= p(-2)=0.

FACTORS OF POLYNOMIAL
The steps are given below to find the factors of a polynomial using factor theorem: Step 1 : If f(-c)=0, then (x+ c) is a factor of the polynomial f(x). Step 2 : If p(d/c)= 0, then (cx-d) is a factor of the polynomial f(x). Step 3 : If p(-d/c)= 0, then (cx+d) is a factor of the polynomial f(x).

The value of the polynomial at a point is defined as the value obtained at a specific point for the given function. For example, let the polynomial function be P(x)= x+1. Therefore, the value of the polynomial P(X) at x= 1 is 2

POLYNOMIALSf(x) = a1 + a1x + a1 x²....... a1x²