Transformaciones y Distribuciones Muestrales
Teoremas de transformación
para variables aleatorias (X)
Primer Teorema
Se tiene función de densidad de X fX(x)
φ:(a,b) una función continua, creciente o
decreciente y con inversa diferenciable
Y=φ(x) dentro de φ(a,b)
La función de densidad de Y es:
fY(y)=fX(φ-1(y))|(φ-1(y))'|
Segundo Teorema
X∈(a,c) con función de densidad fX(x)
Y=φ(x)={
φ1(x), x∈(a,b)
Ambas funciones continuas, crecientes o
decrecientes y con inversas diferenciables,
a<b<c
La función de densidad de Y es:
fY(y)=fX(φ1-1(y))|(φ1-1(y))'|+fX(φ2-1(y))|(φ2-1(y))'|
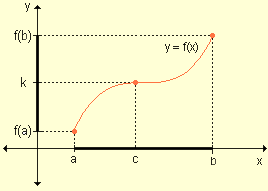
φ2(x), x∈(b,c)
Tercer Teorema
(X,Y) vector continuo en los reales
Función de densidad del vector (X,Y)
es fX,Y(x,y)
(U,V)=φ(x,y) dentro de φ(I)
Función de densidad del vector (U.V)
fU,V(u,v)=fX,Y(φ1-1(u,v),φ2-1(u,v))|J(u,v)|, (u,v)∈φ(I)
Pasos para aplicarlo
1. Identificar fX,Y(x,y) y su dominio
2. Identificar la transformación
φ(x,y)=(U,V)
U=φ1(x,y)
V=φ2(x,y)
3. Obtener las funciones inversas y calcular el Jacobiano
X=φ1-1(u,v)
Y=φ2-1(u,v)
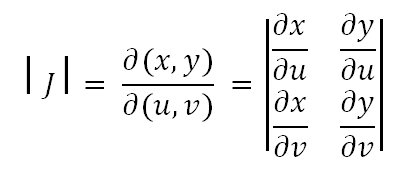
Fórmula para calcular el Jacobiano de (U,V)
4. Determinar fU,V(u,v)
5. Determinar el dominio de (U,V)
Vectores de Transformación
Distribución de la suma
X1,X2,...,Xn∼N(μ,σ2)
fXY(u)=∫fX,Y(u-v,v) definida en u
Distribución de la resta
X1-X2∼N(μ1-μ2,σ12+σ22)
fXY(u)=∫fX,Y(u+v,v) definida en u
Distribución del producto
fXY(u)=∫fX,Y(u/v,v)|1/v|dv definida en u
Distribución del cociente
fX/Y(u)=∫fX,Y(uv,v)|v|dv definida en u
Muestras Aleatorias
Colección de variables aleatorias, todas ellas
independientes e idénticamente distribuidas
s2
Esperanza
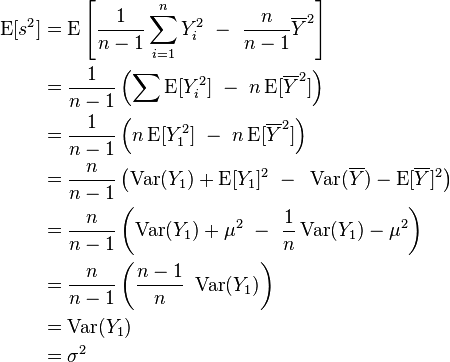
Varianza
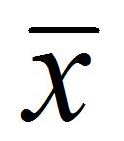
Esperanza

La esperanza de x barra toma el valor de μ
Varianza
La varianza de x barra toma el valor de σ2/n1/2
Proposiciones de las
Distribuciones Muestrales
Si X∼N(0,1)
X2∼x2(1)
Si X1, X2, ..., Xn son iid, con Xi∼x2(ni)
para i=1, 2, ..., m
∑Xi∼x2(n1+...+nm)
sumando desde i=1 hasta n
Si X1, X2, ..., Xn son iid, con Xi∼N(μ,σ2)
∑(Xi-μ)2/σ2∼x2(n)
sumando desde i=1 hasta n
∑Xi2(1)∼x2(n)
sumando desde i=1 hasta n
X y Y independientes, con X∼x2(n),
X+Y∼x2(m)
Y∼x2(m-n)
Sean X1,...,Xn iid, Xi∼N(μ,σ2)
s2(n-1)/σ2∼x2(n-1)
Estadísticos
Cualquier función que depende de las variables X1, X2, ..., Xn
Media muestral
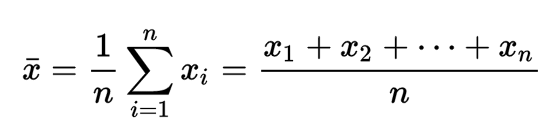
Varianza muestral
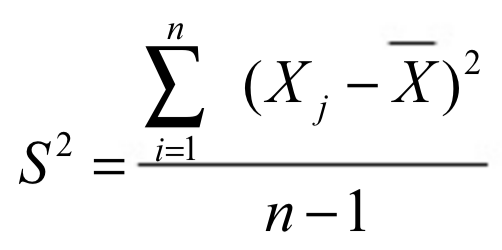
Rango
R=X(n)-X(1), donde n es el tamaño de la muestra
Mediana
Fórmula para n impar:
Me=X((n+1)/2)
Fórmula para n par
Me=[X(n/2)+X((n+1)/2)]/2