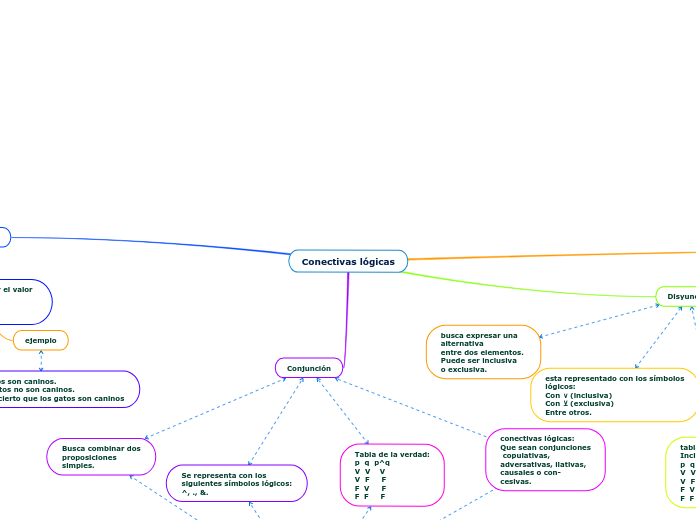
Busca presentar dos
enunciados
con relación
antecedente-
consecuente.
Este, busca invertir el valor
de la verdad de
la expresión a la
qué se le aplica.
Se representa con los siguientes símbolos
lógicos: ¬p, -p,
~p, p y Np.
Conectivas lógicas: No, negativa,
jamás, nada,
nunca, entre
otras.
p: Los gatos son caninos.
¬p: Los gatos no son caninos.
¬p: No es cierto que los gatos son caninos
Se representa con los
siguientes símbolos lógicos:
^, ., &.
Busca combinar dos
proposiciones
simples.
conectivas lógicas:
Que sean conjunciones
copulativas,
adversativas, ilativas,
causales o con-
cesivas.
Tabla de la verdad:
p q p^q
V V V
V F F
F V F
F F F
ejemplo:
p: los perros ladran.
q: Los gatos maullan.
p^q: Los perros ladran y los gatos maullan.
p^q: Los perros ladran, pero los gatos maullan.
busca expresar una
alternativa
entre dos elementos.
Puede ser inclusiva
o exclusiva.
esta representado con los símbolos
lógicos:
Con ∨ (inclusiva)
Con ⊻ (exclusiva)
Entre otros.
conectivas lógicas
principalmente:
o (inclusiva)
o bien (exclusiva)
tabla de la verdad:
Inclusiva Exclusiva
p q p∨q p q p⊻q
V V V V V F
V F V V F V
F V V F V V
F F F F F F
ejemplo:
p: Ayer salí a correr.
q: Ayer hice tareas
pvq: Ayer salí a correr o hice tareas.
p⊻q: Ayer salí o bien a correr o bien hice tareas
se presenta:
Con los símbolos
lógicos: ⇒, →, ⊃.
Conectivas lógicas:
Entonces, por
consiguiente,
implica, es obvio
que, entre otros.
tabla de la verdad:
p q p→q
V V V
V F F
F V V
F F V
ejemplo:
p: 1x + 4 = 5
q: x = 1
p → q: Si 1x + 4 = 5, entonces x=1.