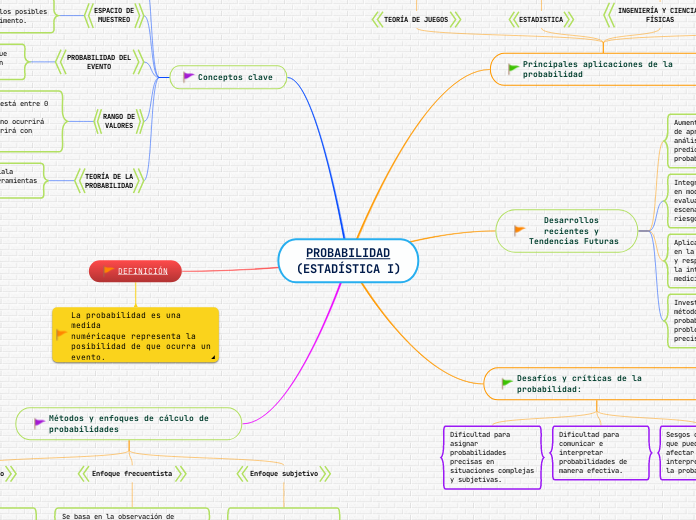
PROBABILIDAD
(ESTADÍSTICA I)
Principales aplicaciones de la probabilidad
TEORÍA DE JUEGOS
Estudia las estrategias óptimas y las
probabilidades de distintos resultados
en situaciones de decisión.
ESTADISTICA
Utiliza la probabilidad para analizar
datos y hacer inferencias sobre una población.
INGENIERÍA Y CIENCIAS
FÍSICAS
Utiliza la probabilidad para modelar sistemas
complejos y predecir eventos futuros.
FINANZAS Y GESTIÓN
DE RIESGOS
Utiliza la probabilidad para evaluar y
gestionar los riesgos financieros.
Desarrollos recientes y Tendencias Futuras
Aumento en el uso de técnicas de aprendizaje automático y análisis de datos para hacer predicciones basadas en probabilidades.
Integración de la probabilidad en modelos de simulación para evaluar el impacto de diferentes escenarios en situaciones de riesgo.
Aplicación de la probabilidad en la toma de decisiones éticas y responsables en campos como la inteligencia artificial y la medicina.
Investigación continua en nuevos métodos de cálculo y análisis de probabilidades para abordar problemas complejos y mejorar la precisión de las estimaciones.
Desafíos y críticas de la probabilidad:
Dificultad para asignar probabilidades precisas en situaciones complejas y subjetivas.
Dificultad para comunicar e interpretar probabilidades de manera efectiva.
Sesgos cognitivos que pueden afectar la interpretación de la probabilidad.
Conceptos clave
EVENTO
Un suceso o resultado que se puede
observar o experimentar.
ESPACIO DE
MUESTREO
PROBABILIDAD DEL
EVENTO
RANGO DE
VALORES
TEORÍA DE LA
PROBABILIDAD
Un campo matemático que estudiala
probabilidad y proporciona herramientas
para calcularla y analizarla.
DEFINICIÓN
Métodos y enfoques de cálculo de probabilidades
Enfoque clásico
Enfoque frecuentista
Se basa en la observación de frecuencias
relativas de eventos en el pasado para
estimar la probabilidad de eventos futuros.
Enfoque subjetivo