Forms of Quadratic Equations
a = vertical stretch/compression factor
Sub in x as 0 to find y-intercept
If a > 1 or a < -1, then the graph is stretched vertically by a
factor of a
Direction of Opening
-----------------------
If a>0 it is upward opening parabola, if a<0 it is downward opening parabola
y=0.5(x-6)(x+2)
y=0.5(0-6)(0+2)
y=0.5(-6)(2)
y=0.5(-12)
y=(-6)
Y-intercept is (0,-6)
Binomials (x-r) and (x-s) gives the x-intercepts
Solve each binomial individually for x to get the x-intercept(s)
adding x-intercepts and then dividing by 2 = axis of symmetry - midpoint of x-intercepts
y=0.5(x-6)(x+2)
--------------------------
x-6=0 x+2=0
x=6 x=-2
x1= (6,0) x2= (-2,0)
(6,0) and (-2,0)
------------------
=[6+(-2)]/2
=[4]/2
=2
Axis of Symmetry is (2,0)
c value is the y-intercept of a parabola
a, b and c are all known values
x is the unknown variable - a value is never 0
If -1 < a < 0 or 0 < a < 1, (a is a fraction)then the graph is compressed vertically
Sub in x=0 to find y-intercept
h = x value of the vertex and axis of symmetry
"h" represents a horizontal shift
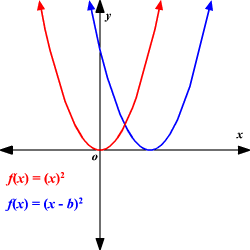
If h>0, it is a horizontal shift to the right. If h<0, it is a horizontal shift to the left
k = y value of the vertex
"k" represents a vertical shift

If k>0, it is a vertical shift up by k units. If k<0, it is a vertical shift down by k units.
Solving Quadratic Equations
Finding x-intercepts from Standard Form using Quadratic Formula
X-intercepts/Roots/Zeroes = Solutions
Convert Standard Form to Vertex Form and find Maximum/Minimum values or vertex of parabolas
y=3x² -12x-5
y=(3² -12x)-5
y=3(x² -4x)-5
-4/2=-2² =4
y=3(x² -4x+4)-5
y=3(x² -4x+4)-17
y=3(x-2)² -17
Vertex = (2,17) Minimum = -17
Negative discriminant = no real roots
If discriminant is zero there is 1 root
Positive discriminant = 2 roots
x = -b ± √b² - 4ac
________________
2a
0=60x-2x²-400 x=-60± √60² - 4(-2)(-400)
_________________
2(-2)
x=-60± √400
___________
2(-2)
Used to turn a quadratic into factored form to solve equation by finding X-intercepts
Trinomial Standard Form
ax² +bx+c
----------------------------
2x² +10x-12
=2(x² +5x-6)
=2(x² -1x+6x-6)
=2(x(x-1)+ 6(x-1)
=2(x-1)(x+6)
Simple Trinomials- (x+m) (x=n)
If the trinominal cannot be common factored and the a value is more than 1, you have to multiply a and c
1. Common Factor (If Any)
Common Factor = 2
2. Factor by Grouping (if necessary)
Group terms with common factors to solve
2x² +6y+4x+3xy
=2x² +4x+6y+3xy
=2x(x+2)+3y(2+x)
=(x+2)(2x+3y)
=x² +nx+mx+mn =x² +x(n+m) +mn =x² +(m+n)x +mn
3. Two numbers
-Multiply to "c"
-Add to "b"
Complex Trinomial: a≠1
=2x² -26x-24
=2 [x²-13x+12]
=2 (x-12)(x-1)
Decomposition
1. Multiply (a)(c)
2. Break down middle term
3. Group Factoring (always add)
4. Common Factoring
=2x² -26x-24
=2x² -2x - 24x +24
=(2x²-2x) + (-24+24)
=2x(x-1) + -24(x-1)
=(x-1) (2x-24)
=2 (x-1)(x-12)
Domain and Range
f(x)= 3 (x-2)²+3
D:{xeR}
R:{yeR/y≥ 3}
Expanding Quadratic Functions
Perfect Square Trinomials
( x + a ) ( x – a ) = x² – a²
( x + 5 ) ( x – 5 )
= x² – 5x + 5x – 25
= x² – 25
Middle term cancel out
Sub. in x and a values to expand
First Outside Inside Last
( x + 3 ) ( x + 2 )
= x^2 + 2x + 3x + 6
= x^2 + 5x + 6
( x + a )² = x² + 2ax + a²
( x – a )² = x² – 2ax + a²
When the Binomial is square, to expand you must multiply the binomial by itself
1. Get rid of the square sign and have the binomials multiply eachother
( x – 3 ) ( x – 3 )
= ( x + 5 )²
= ( x + 5 ) ( x + 5 )
= x² + 10x + 25
Finite Differences in Quadratic Relations
FD = Subtracting consecutive y-values
If First Differences are constant, there is a linear relation
If Second Differences are constant, there is a quadratic relation
SD = Subtracting FD values
If FD or SD are not constant, the relation is niether