Quadratics
First and second differences The purpose of the first and second difference is to find the properties of the relation
Quadratic equations
parabolas
Parabolas can open up and down. The Y intercept of a parabola is where the graph crosses the Y axis. The zero is also called the X intercept or the root. The axis of symmetry divides the parabola into 2 equal halfs. The vertex of a parabola is the point where the axis of symmetry and the parabola meet, it is the point where the parabola is at its maximum or minimum value. The optimal value is the value of the Y coordinate of the vertex. The X intercept of a parabola is where the graph crosses the X axis
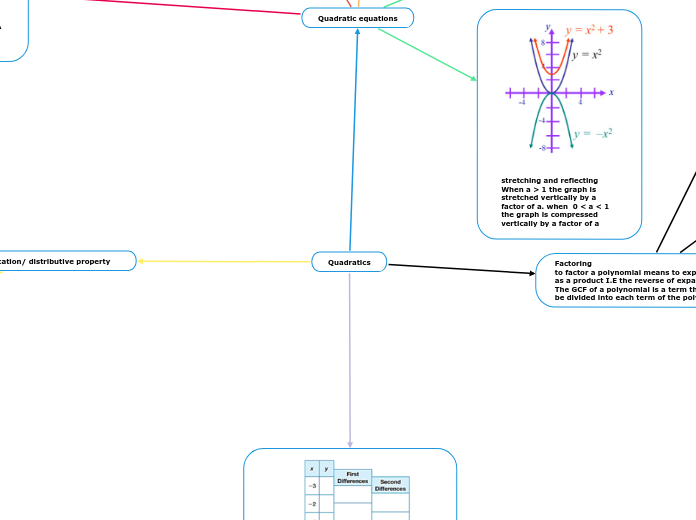
translating a(x - h)^2 + k. If h > 0 the graph shifts to the right and if h<0 it shifts to the left
equations Quadratic Equations are in the form Ax^2 + bx + c = 0 where a,b,c are in the set of real numbers and a does not =0. The solution to a quadratic equation is known as the roots/zeros of the equation. A quadratic equation may have two distince real roots, two equal real roots or no real roots.
zero product property If the product of two real numbers is zero, then one or both of the numbers must equal 0. If xy=0, then either x = 0 or y = 0. If X(x+3) = 0 then either x=0 or X + 3 = 0. If 3(x+2_(x-2) = 0, then either x+2 = 0 or X - 2 = 0
Step pattern is the quickest and most effcient way to graph quadratic relations in Y = a(x-h)2 + k. use the numbers 1,3,5. you start by going up by 1 over one then up by 3 and over 1 then up 5 and over 1.
Solving
Standard form to vertex form 1. each of the factors equal to zero 2. solve for x 3. find the axis of symmentry and the X coordinate of the vertex from the midpoint between zeros 4. substitute this X value into the relation to find the Y coordinate of the vertex. If you cannot completly factor it you can express the relation in partially factored from Y = x(ax + b) + c, then this form may be used to determine the vertex. 1. In the relation y = ax2 + bx + c, let y = c and solve for x
2. Common factor x from the first two terms of the standard equation
3. Set x(ax + b) = 0.
4. Solve for x to determine two points on the parabola that are the same distance from
the axis of symmetry. Both of these points have the y-coordinate c.
5. Determine the axis of symmetry, x = h, by calculating the mean (midpoint) of the
x-coordinates of these two points.
6. Substitute x = h into the relation to determine k, the y-coordinate of the vertex.
Quadratic formula The roots of any quadratic in the form Ax^2 +bx + c = 0 can be found using the quadratic formula. If the formula leads to a negative number under the square root sign. when this happens that means the relation has no real roots.
Binomial multiplication/ distributive property
FOIL method
Factoring to factor a polynomial means to express it as a product I.E the reverse of expanding. The GCF of a polynomial is a term that can be divided into each term of the polynomial.
Factoring trinomials
simple trinomials Any trinomial in the form X^2 + bx + c is called a simple quadratic trinomial and can be factored in the following ways: 1. Determine what two integers have a product of c and a sum of b 2. Write two brackets side by side. inside each bracket write an X as the first term and the two integers as the second terms.
complex trinomials Any trinomial in the form Ax^2 +bx + c where A does not equal one is called a complex quadratic trinomial and can be factored in the following way: 1. Determines what two integers have a product of ac and a sum of b 2. break up the middle of the trinomial using the two integers 3. common factor by grouping
special cases
Difference of squares The expamded experession is called a difference of squares. both terms are perfect squares and the terms are seperated by a minus sign.
Perfect square trinomials In a perfect square trinomial, the first and last terms are perfect squares, and the middle term is twice the product of the square roots of the first and last terms
Factored form of a parabola Y = a(X - S)(x - t)