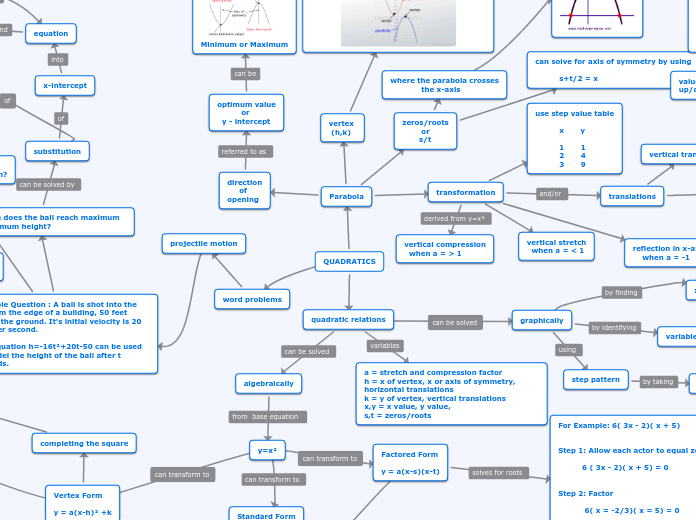
QUADRATICS

quadratic relations

algebraically

y=x²

Standard Form

y = ax²+bx+c

a = stretch and compression factor
h = x of vertex, x or axis of symmetry, horizontal translations
k = y of vertex, vertical translations
x,y = x value, y value,
s,t = zeros/roots

Parabola

direction
of
opening

optimum value
or
y - intercept

vertex
(h,k)

zeros/roots
or
s/t

where the parabola crosses
the x-axis

can solve for axis of symmetry by using

s+t/2 = x

transformation

vertical compression
when a = > 1

vertical stretch
when a = < 1

translations

vertical translation

value of 'k' determines units shifted up/down

horizontal translation

value of 'h' determines units shifted left/right

reflection in x-axis
when a = -1

use step value table

x y

1 1
2 4
3 9

word problems

projectile motion

x= −b±√b²-4ac
__________
2a

a quadratic equation cannot be factored

Vertex Form

y = a(x-h)² +k

completing the square

For Example: y = 2x² + 12x - 3

Step 1: remove common factor from x² and x-term

y = 2( x² + 6x ) - 3

Step 2: find the value of half the x-term coefficient. This value squared is equal to the constant that needs to be added and subtracted to make a perfect square.

a) (6/2)²


b) y = 2( x² + 6x + 9 - 9 ) - 3


Step 3: group the terms that make the perfect square. Move the subtracted value outside the brackets by multiplying it by the common factor.

y = 2( x² + 6x + 9 ) - 18 - 3


Step 4: factor and collect like-terms.


y = 2( x + 3)² - 21

to solve: isolate for 'x'

y = 2(x - 1)² + 5

Step 1: Move 'k' to other side of equal sign. It is now negative.

-5 = 2( x -1)²



Step 2: Move 'a' to other side of equal sign. It's function changes from multiplication to division.

-5/2 = (x - 1)²


Step 3: Solve left side, while finding the square root of the right side of equal sign.

-5/2 = √(x - 1)²

↓

-2.5 = (x- 1)


Step 4: Rearrange sides of the equal sign

(x-1) = -2.5



Step 5: Isolate 'x' by moving -1 to the other side of equal sign. -1 then becomes positive.

x = -2.5 + 1


Step 6: Solve.

∴ x = -1.5

Factored Form

y = a(x-s)(x-t)

For Example: 6( 3x - 2)( x + 5)


Step 1: Allow each actor to equal zero

6 ( 3x - 2)( x + 5) = 0


Step 2: Factor

6( x = -2/3)( x = 5) = 0


∴ x = 2/3

x = -5

factoring

1. Common factor

For Example: 4x² - 48x + 144



Step 1: Find the G.C.F → 4


Step 2: Divide each term by G.C.F


4(x² - 12x + 36)


Step 3: Factor fully using the ABC method



a = 1 -6 x -6 = 36



b = -12 -6 + -6 = -12



c = 36



∴ ( x - 6 )(x - 6)

2. Trinomials

simple

a = +1

For Example: x² + 9x + 20



Step 1: Start with an 'x' in each bracket



( x ) (x )


Step 2: Use the ABC method to solve



a = 1 4 x 5 = 20



b = 9 4 + 5 =9



c = 20


∴ ( x + 4 ) ( x + 5 )

complex

a is not equal to +1

For Example: 6x² + 13x + 5



Step 1: Use the ABC method


a = 6 10 x 3 = 30



b = 13 10 + 3 = 13



c = 5


Step 2: break down 'b' or middle term


6x² + 10x + 3x + 5


Step 3: group terms


2x(3x + 5 ) + 1(3x + 5)


Step 4: factor out G.C.F from each group



(3x + 5) ( 2x + 1)


∴ x = 5/3
x = 1/2

3. difference of squares

a² - b²

OR

√(a+b) √(a-b)

x² - 9

Step 1: Find square root

√(x² + 9) √(x² - 9)

Step 2: ( x + 3 ) ( x - 3)

∴ x = -3
x = 3

* to check answer: expand using F.O.I.L*

quadratic formula

Discriminant

3 possibilities

0 real roots

√b²-4ac < 0

1 real root

√b²-4ac =0

2 real roots

√b²-4ac >0

√b²-4ac

is use to find ( h,k ) which is the vertex

horizontal shifts ( left, right)

vertical shits ( up,down)

Step 1: x= -5±√25+24
__________
4

Step 2: x= -5±√49
_______
4


Solve for negative √ x = -5 -√49
______
4

x = -3


Solve for positive √ x= -5 + √49
_______
4

x = 0.5

graphically

x-intercepts

graph

zeros/roots

zeros/roots

For Example: y=x²+2x-3

Step 1: Use x=-b/2a to find axis of symmetry

x=-2/2(1), x=1

Step 2: Sub x=1 into equation to find
y-intercept

y=(1)²+2(1)-3, y=-4

So vertex is (1,-4)

Step 3: sub x=0 into equation to find
y-coordinate to create another point

y=(0)²=2(0)-3, y=-3

2nd coordinate, (o,-3)

Step 4: Plot axis of symmetry, x=1
Plot vertex, (1,-4)
Plot 2nd coordinate, (0,-3)

Step 5: coordinates even, then connect the dots

variables a,b,c

axis of symmetry

x= -b/2a

x-value

equation

coordinates

vertex

x=0

equation

coordinates

2nd coordinate

step pattern

'a'

vertex form

y
1
4
9

coordinates

Example: y=-2x²+9
x y

1 1x2, (1,2)
2 4x2, (2,8)
3 9x2, (3,18)

graph

Example Question : A ball is shot into the air from the edge of a building, 50 feet above the ground. It's initial velocity is 20 feet per second.

The equation h=-16t²+20t-50 can be used to model the height of the ball after t seconds.

at what time does the ball reach maximum height? Minimum height?

substitution

x-intercept

equation

max/min height

About how long does it take for the ball to hit the ground?

quadratic formula

x= −b±√b²-4ac
__________
2a

x-intercept

at what time will the ball
have a height of exactly 35m?

substitution

equation

time/x-intercept