If the height is less than the b value, then it is an ambiguous case
The CAST rule applies to the special angles alongside with all other angles
Geometric is derived from the growth model
Annuities formulas are derived from Geometric sum
Cosine waves are sine waves but phase shifted 90 degrees to the left
3D problems are just many 2D problems
Expanded form
Where growth is in %, not doubling

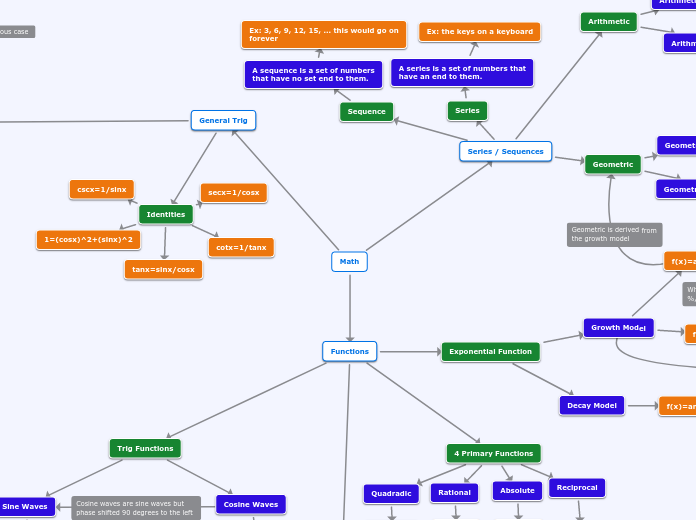
Math

Functions

Trig Functions

Sine Waves

f(x)=asin(k(x-h))+c

(x,y)---}((x/k)+h,ay+c)

Cosine Waves

f(x)=acos(k(x-h))+c

(x,y)---}((x/k)+h,ay+c)

4 Primary Functions

Quadradic

f(x)=x^2

Rational

f(x)=√x

Absolute

f(x)=|x|

Reciprocal

f(x)=1/x

Exponential Function

Decay Model

f(x)=ar^x (where r is a decimal / fraction)

Growth Model

f(x)=ar^x

f(x)=A₀(1+i)^x

Function Definitions

Discrete:

A function that has specific data set.
Aka: several points in data.

Ex: # of students in a class, only a set #
as you cannot have 1/2 of a student.

Recursive:

A function that calls upon previous
numbers within the function.

Ex: the Fibonacci sequence that
uses the previous numbers in the sequence
to make the new number.

tn=t(n-1)....

Continuous:

A function where numbers can be
any value within a set.

Ex: time it took to complete some task
at any point you could say 1/2 of a second,
1 microsecond,
1 minute but there is a defined set if the task for example took 10 minutes.

General Trig

Identities

tanx=sinx/cosx

secx=1/cosx

cscx=1/sinx

cotx=1/tanx

1=(cosx)^2+(sinx)^2

Trig Problems

3D Problems

Ambiguous Case

h=asinB

2D Problems

Special Angles

Angles for: 30° and 60°

Angles for: 30° and 60°

Angles for 45°

Angles for 45°

Unit circle

This is the CAST rule

This is the CAST rule

Series / Sequences

Series

A series is a set of numbers that
have an end to them.

Ex: the keys on a keyboard

Sequence

A sequence is a set of numbers
that have no set end to them.

Ex: 3, 6, 9, 12, 15, ... this would go on
forever

Arithmetic

Arithmetic Series / Sum Formula

Sn=n(a+tn)/2

Sn=n(2a+d(n-1))/2

Arithmetic Sequence

a+d(n-1)

Geometric

Geometric Sequence

ar^n-1

Geometric Series / Sum Formula

Sn=a(r^n-1)/r-1

Financial Applications

Annuities

Present Value

PV=R(1-(1+i)^-n)/i

PV=R(1-(1+i)^-n)/i

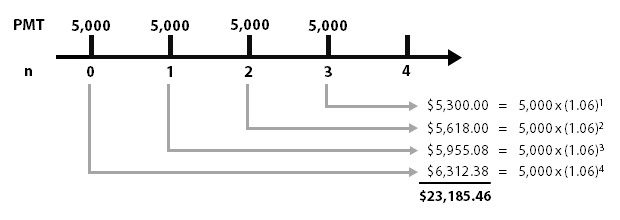
Future Value

FV=R(((1+i)^n)-1)/i

FV=R(((1+i)^n)-1)/i

Annuities are compounding
interests where you are
adding more money into
the account as time goes
on, alongside with the
interest earned on the money
from before.

Compounding Interest

A=P(1+i)^n

The interest is the rate, r,
by the compounding period.

The time, n, is
the amount of time multiplied
by the compounding period.

Simple Interest

I=Prt

A=P+I