Algebra Lineal
¿Qué estudia?
Espacios vectoriales

es un conjunto de objetos, denominados vectores, junto con dos operaciones binarias llamadas suma y multiplicación por un escalar y que satisfacen los diez axiomas enumerados a continuación.
Espacios vectoriales conproducto interno
es una operación que asigna a cada par de vectores u y v en V un número real <u, v>. ii. (v, v) = 0 si y sólo si v = 0.
Transformaciones lineales
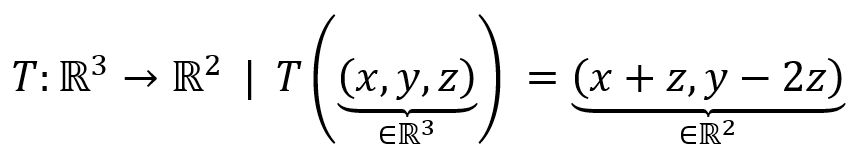
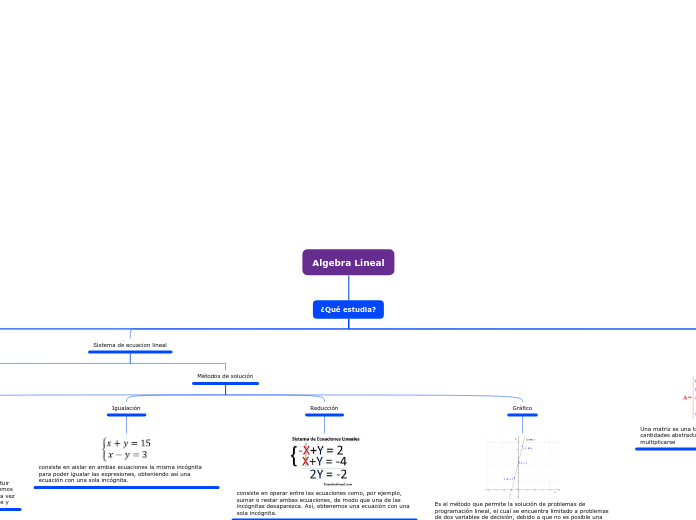
Son transformaciones entre espacios vectoriales que conservan la suma vectorial y la multiplicación por escalar.

Los vectores propios son vectores multiplicados por un valor propio en las transformaciones lineales de una matriz.
Caracteristicas
Diagonal ortogonal
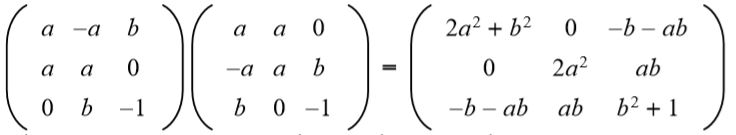
Forma cuadratica

La forma cuadrática matricial es el producto de la multiplicación de un vector de orden n con una matriz cuadrada cualquiera por el vector de orden n traspuesto.
Matriz simétrica

Una matriz es simétrica si es una matriz cuadrada, la cual tiene la característica de ser igual a su transpuesta.
Matrices semejantes
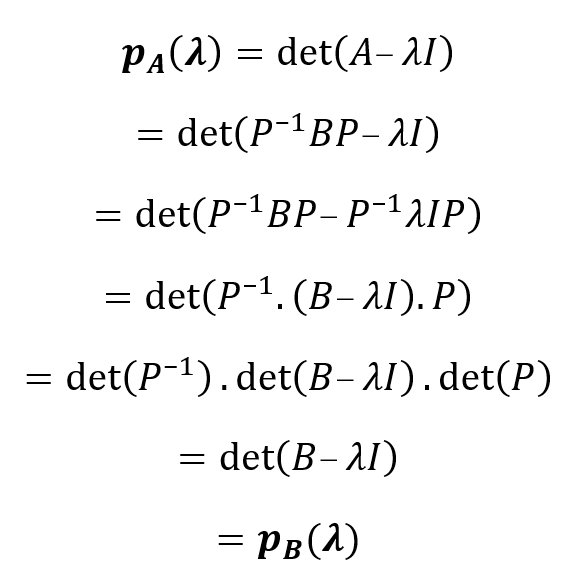
Se dice que las matrices NxN, A y B son semejantes o similares si existe una matriz C invertible
Sistema de ecuacion lineal

Un sistema lineal son agrupaciones de ecuaciones de primer orden con las mismas incógnitas que deben encontrar una solución común. Un sistema puede contener m ecuaciones y n incógnitas, y su solución es única con infinitas posibilidades o sin respuestas.
Métodos de solución
Sustitución

consiste en despejar o aislar una de las incógnitas y sustituir su expresión en la otra ecuación. De este modo, obtendremos una ecuación de primer grado con la otra incógnita, y. Una vez resuelta, calculamos el valor de x sustituyendo el valor de y
Igualación

consiste en aislar en ambas ecuaciones la misma incógnita para poder igualar las expresiones, obteniendo así una ecuación con una sola incógnita.
Reducción
consiste en operar entre las ecuaciones como, por ejemplo, sumar o restar ambas ecuaciones, de modo que una de las incógnitas desaparezca. Así, obtenemos una ecuación con una sola incógnita.
Gráfico

Es el método que permite la solución de problemas de programación lineal, el cual se encuentra limitado a problemas de dos variables de decisión, debido a que no es posible una representación gráfica de más de tres dimensiones.
Matriz

Una matriz es una tabla bidimensional de números en
cantidades abstractas que pueden sumarse y
multiplicarse
Tipos de Matrices
Matriz Nula
Tiene todos los
elementos cero
Matriz Fila

Matriz Columna
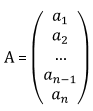
Matriz Cuadrada

Matriz Rectangular
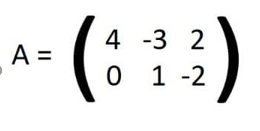
Subtopic
Determinantes
Propiedades
Inversa
Teoremas
Regla de Cramer
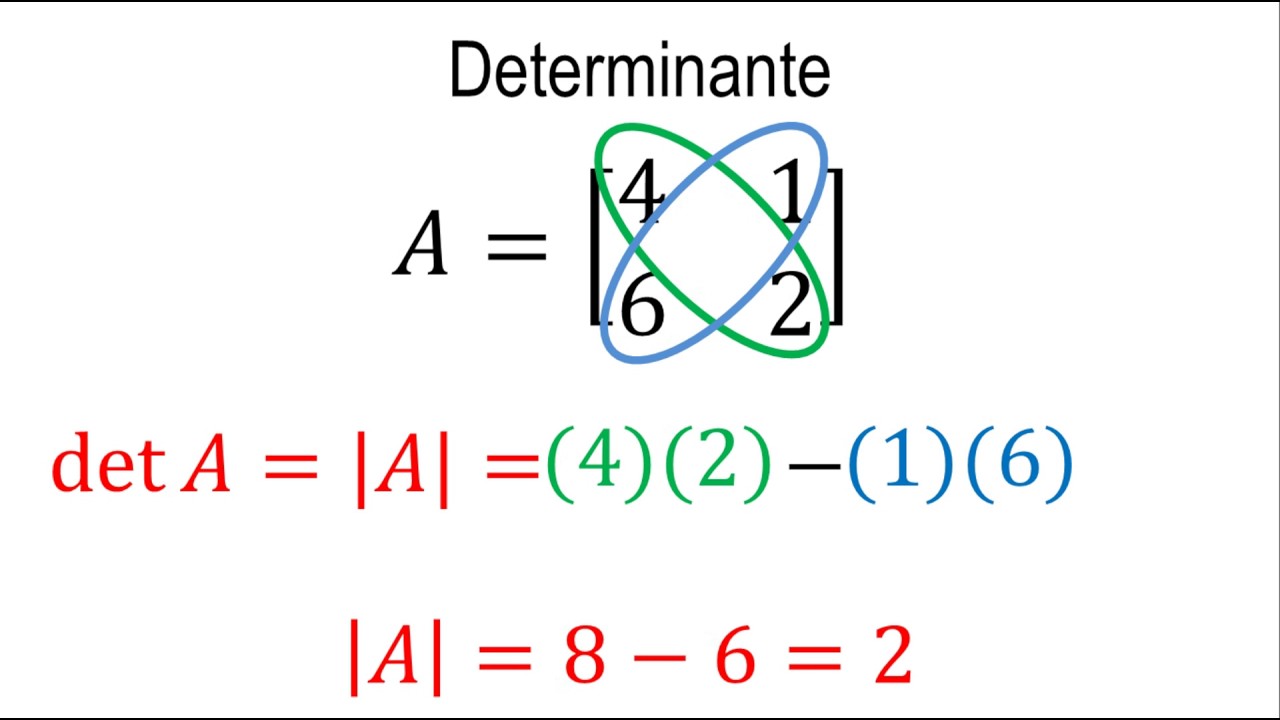
El determinante es una herramienta matemática que puede extraer o encontrar un determinante en las matrices cuadradas (las matrices cuadradas tienen la misma cantidad de numero de filas y columnas) el cual es un numero real y consiste en la suma de productos elementales de la matriz.
Números Complejos
Un número complejo es un número de la forma a+bi donde a y b son números reales e i es un símbolo con la propiedad de que i' =-1.
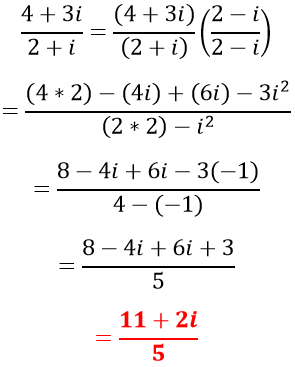
Operaciones elementales con números complejos

Representación de un número complejo z en el plano complejo
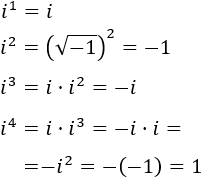
Operaciones
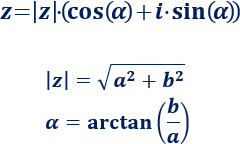
Forma Polar
Sean r y θ coordenadas polares del punto (x, y) que corresponde a un número complejo no nuloz = x + iy.Comox = r cos θey = r sen θz puede ser expresado en forma polarcomoz = r(cosθ+ i senθ).En análisis complejo, no se admitenrnegativos; sin embargo, como en el Cálculo,θtiene infinitos valores posibles, incluyendo valores negativos.

Potencias de “i”, módulo o valor absoluto de un número complejo