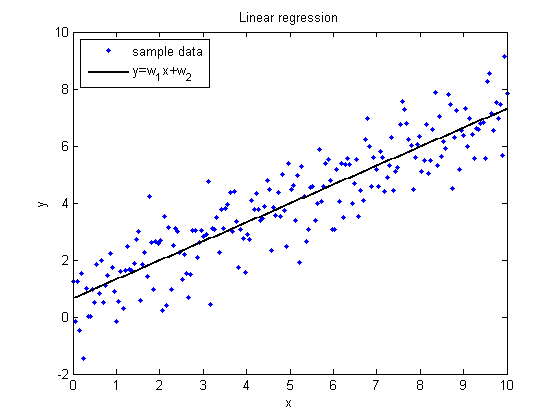
регрессионная модель

Регрессионная модель [reg­res­sion model] — экономико-статистическая модель, основанная на уравнении регрессии, или системе регрессионных уравнений, связывающих величины экзогенных (входных, «объясняющих») и эндогенных (выходных) переменных.

Основные предпосылки для применения модели:

Виды моделей:

Недостатки регрессионного анализа: модели, имеющие слишком малую сложность, могут оказаться неточными, а модели, имеющие избыточную сложность, могут оказаться переобученными.

Переобучение(overtraining) — нежелательное явление, возникающее при решении задач обучения по прецедентам, когда вероятность ошибки обученного алгоритма на объектах тестовой выборки оказывается существенно выше, чем средняя ошибка на обучающей выборке.

К достоинствам данных моделей прогнозирования относят: простоту, гибкость, а также единообразие их анализа и проектирования [19]. При использовании линейных регрессионных моделей результат прогнозирования может быть получен быстрее, чем при использовании остальных моделей. Кроме того, достоинством является прозрачность моделирования [5], т. е. доступность для анализа всех промежуточных вычислений.

2. Множественная линейная регрессия - задача предполагает установление линейной зависимости между группой независимых переменных Х1,Х2, … ХК и одномерным откликом у. Стратегия анализа адекватности подобранной модели в задаче мно­жественной регрессии в целом аналогична задаче простой регрессии и сводится к детальному анализу остатков.

При решении задач множественной регрес­сии самым главным является выбор тех переменных, которые оказывают существенное влияние на отклик, и отсеивание несущественных переменных. Для этого используют очень эффективные на практике методы шаговой регрессии.

3. Нелинейная регрессия.В этом случае параметры модели входят в подбираемую регрессионную функцию нелинейным образом. Нахождение их оценок в этом случае представляет собой более сложную задачу.

1. Простая линейная регрессия - самый простой случай - установление линейной связи между одной независимой (одномерной) переменной х и одной зависимой переменной (откликом) у.

4. Множественная нелинейная регрессия- ещё более сложная задача, так как в данном случае нелинейность может сочетаться с взаимодействием факторов. Существует мнение, что использование методов нелинейной регрессии, особенно множественной нелинейной регрессии, оправдано лишь в том случае, когда вид регрессионной зависимости известен априори. Однако опыт показывает, что при наличии современных быстродействующих программных средств и известной осторожности в применении (постоянное использование t-критерия и сравнения достоверности разных моделей) такая регрессия может оказаться очень эффективной. Она в ряде случаев позволяет обнаружить новые закономерности, которые лишь впоследствии находят теоретическое объяснение.

1. Нулевое математическое ожидание ошибок;

2. Диагональность ковариационной матрицы ошибок;

3. Отсутствие гетероскедастичности в модели.

Нарушение любой из этих предпосылок ведет к искажению полученных результатов. Можно не обнаружить существующую зависимость или построить ложную модель. Поэтому, за кажущейся простотой метода скрывается целый комплекс проблем, неочевидных на первый взгляд.

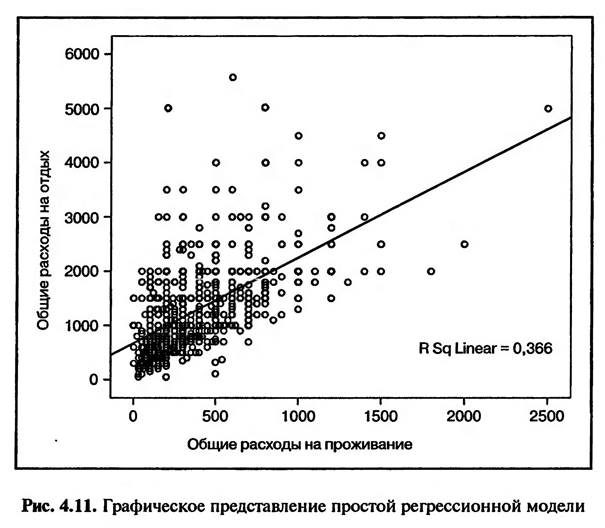
Линейная регрессия (англ. Linear regression) — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной
y
y от другой или нескольких других переменных (факторов, регрессоров, независимых переменных)
x
x с линейной функцией зависимости.