Polynomial Function
x and y intercepts
The graphical concept of x- and y-intercepts is pretty simple. The x-intercepts are where the graph crosses the x-axis, and the y-intercepts are where the graph crosses the y-axis. The problems start when we try to deal with intercepts algebraically.
Find the x- and y-intercepts of 25x2 + 4y2 = 9
Using the definitions of the intercepts, I will proceed as follows:
x-intercept(s):
y = 0 for the x-intercept(s), so:
25x2 + 4y2 = 9
25x2 + 4(0)2 = 9
25x2 + 0 = 9
x2 = 9/25
x = ± ( 3/5 )
Then the x-intercepts are the points ( 3/5, 0) and ( –3/5, 0) y-intercept(s):
x = 0 for the y-intercept(s), so:
25x2 + 4y2 = 9
25(0)2 + 4y2 = 9
0 + 4y2 = 9
y2 = 9/4
y = ± ( 3/2 )
Then the y-intercepts are the points (0, 3/2 ) and (0, –3/2 )
Upper and lower bounds
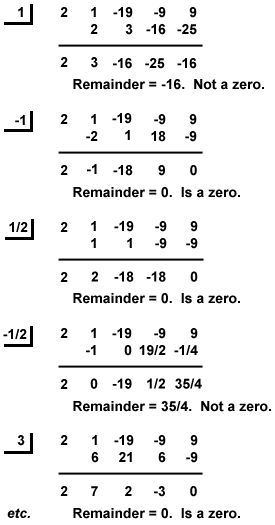
Upper Bound Theorem: If you divide a polynomial function f(x) by (x - c), where c > 0, using synthetic division and this yields all non-negative numbers, then c is an upper bound to the real roots of the equation f(x) = 0. Using synthetic division, I found the integral upper bound to be 2. All the coefficients and the remainder are non-negative.
Now on to the lower bound.
A lower bound is an integer less than or equal to the least real zero.
Lower Bound Theorem:
If you divide a polynomial function f(x) by (x - c), where c < 0, using synthetic division and this yields alternating signs, then c is a lower bound to the real roots of the equation f(x) = 0. Special note that zeros can be either positive or negative.
Using synthetic division again, I tested -1, -2, -3, -4, and -5.
Only -5 yielded alternating signs in the coefficients and remainder of the quotient.
This says that -5 is a lower bound and all the real zeros of can be found in the interval
Now, -4 failed the lower bound theorem test because the quotient did not produce alternating signs. This would suggest that -4 is not a lower bound, right?
However, upon further inspection, the actual zeros are {-3.62, -1.38, 2)
This would seem to indicate that a lower bound (in fact the greatest lower bound) should have been -4.
Multiplicity of a root
For example, in the polynomial function f(x) = (x – 3)4(x – 5)(x – 8)2, the zero 3 has multiplicity 4, 5 has multiplicity 1, and 8 has multiplicity 2. Although this polynomial has only three zeros, we say that it has seven zeros counting multiplicity. See also. Double root, triple root, fundamental theorem of algebra.
A zero has a "multiplicity", which refers to the number of times that its associated factor appears in the polynomial. For instance, the quadratic (x + 3)(x – 2) has the zeroes x = –3 and x = 2, each occuring once.
The turning points
A turning point is a point at which the derivative changes sign. A turning point may be either a relative maximum or a relative minimum (also known as local minimum and maximum). If the function is differentiable, then a turning point is a stationary point; however not all stationary points are turning points.
To find the y-intercept, put x = 0 into the equation and work out the y-coordinate. To find the x-coordinate, put y = 0 in the equation and solve the quadratic equation to get the x-coordinates. To find the vertex (turning point), add the x-intercepts together and divide by 2.
Is a function such as a quadratic, a cubic, a quartic, and so on, involving only non-negative integer power of x.
A polynomial is a function of the form
f(x) = anxn + an−1xn−1 + . . . + a2x2 + a1x + a0 .
The degree of a polynomial is the highest power of x in its expression. Constant (non-zero) polynomials, linear polynomials, quadratics, cubics and quartics are polynomials of degree 0, 1, 2 , 3 and 4 respectively. The function f(x) = 0 is also a polynomial, but we say that its degree is ‘undefined’.
Dividing Polynomials
polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division.
Example: 7x2+x−8x−1
7x2+x−8x−1
You begin by dividing the first term of the dividend (7x2) with the first term of the divisor (x) to find the first term of the quotient (7x) and then you multiply the quotient term with the divisor and subtract.
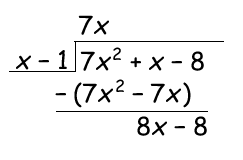
To find the next term of the quotient you just divide the first term of the remaining dividend (8x - 8) with the first term of the divisor (x)
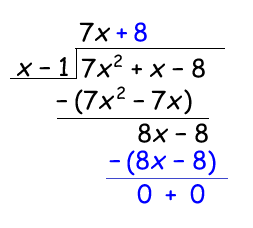
This means that:
7x2+x−8x−1=7x+8
Rational zeros of polynomials
The Rational Zeros Theorem states:
If P(x) is a polynomial with integer coefficients and if p/q is a zero of P(x) ( P(p/q) = 0 ), then p is a factor of the constant term of P(x) and q is a factor of the leading coefficient of P(x) .
Find all the rational zeros of P(x) = x 3 -9x + 9 + 2x 4 -19x 2 .
P(x) = 2x 4 + x 3 -19x 2 - 9x + 9
Factors of constant term: ±1 , ±3 , ±9 .
Factors of leading coefficient: ±1 , ±2 .
Possible values of p/q : ±1/1 , ±1/2 , ±3/1 , ±3/2 , ±9/1 , ±9/2 . These can be simplified to: ±1 , ±1/2 , ±3 , ±3/2 , ±9 , ±9/2 .
Leading coefficient test and its behaviour
The graph of the polynomial function f(x)=anxn+an−1xn−1+...+a1x+a0f(x)=anxn+an−1xn−1+...+a1x+a0 eventually rises or falls depends on the leading coefficient (an)(an) and the degree of the polynomial function.

Example:
Use the Leading Coefficient Test to determine the end behavior of the graph of the polynomial function f(x)=−x3+5xf(x)=−x3+5x .
Solution:
Because the degree is odd and the leading coefficient is negative, the graph rises to the left and falls to the right as shown in the figure.