Elementary Mathematics

Ratios and Proportions

ex. Boys:Girls = 3:515 girls, how many boys?3 boys x boys--------- = ------------5 girls 15 girls45= 5xx=5

Ratio: a:b a over b a to b
Proportion: statement about ratios involving more than one ratio

"=" means same as
ex. 3/4 is the same as 9/12

additive inverse: a+?=0
a+(-a)=0

Problem Solving

Understand the problem

Devise a plan

Look for a pattern

Examine a related problem

Examine a simpler case

Identify a subgoal

Make a table

Make a diagram

Write an equation

Carry out the plan

Look back/ Check the results

Use guess and check

Work backwards

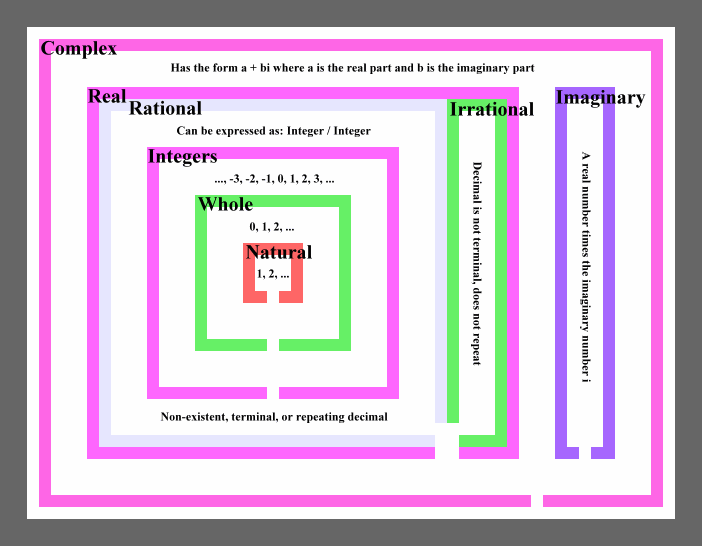
Number Systems

This image shows the different types of numbers including the main ones: natural, whole, integers, rational, irrational and real.

Algorithms

Standard Algorithm:
Standard column by column
ex.
10
+15
------
25

Denominate number:
writing out the places and only adding with same place (noun)

Expanded notation:
ex.
123
+ 10
--------
100+20+3
10+0
-------------
100+30+3= 133

Estimation

Estimation is a way to get an answer similar to the correct one without worrying about all of the minute numbers.

Front-end: ex. 1.50, 2.50, 3.75, 1.25
1+2+3+1= 7
adjust- .50+.50= 1 .75+.25= 1
so..... 7+1+1= 9
Clustering: ex. 500, 501, 499, 502, 498
1. estimate the "average" -about 500
2. multiply the "average" by the number of values
500x5=2500
Rounding: 14x6
about 15x5 which equals 75
Compatible numbers: 27+59+35+65+41+73
27+73=100
59+41=100
35+65=100
= 300
Special numbers: estimating with fractions
ex. 1/2+3/8=1?
no because 3/8 is close to 1/2 but less so it can not equal to one when added to another half

Decimals

10^3 10^2 10^1 10^0 . 10^-1 10^-2 10^-3
1000 100 10 1 . 1/10 1/100 1/1000

Repeating decimals to fractions:

x=.3333
10x=3.3333 -/These cross out
- x= .3333
---------------
9x= 3
--- ---
9 9

x=1/3

Chip Model

Negative in first number means "opposite of"
+
- = 0
(-3) - 2

- - -
++ (these cancel)
- - =(-5)

Bases

This video is a great example of how we have become so accustomed to our base ten system. It would be weird to us if we referred to and counted by base twelve.

Prime Factorization, GCF, LCM

Prime number are numbers that only have the factors 1 and itself.Composite numbers are numbers that have more than two factors.GCF stands for greatest common factorLCM stands for least common multiple

You can use a Venn Diagram to find out the LCM and GCF after finding the prime factoization. To find the GCF you multiply the numbers inside the intersecting circle. To find the LCM you multiply all numbers inside the diagram.b (line) a means that b divides aa=bc IF:-b is a factor of a-a is a multiple of b-b is a divisor of a-a is divisible by b

Fractions

Part-Whole Comparisons with Unitizing:
“3 parts out of 4 equal parts”
Measure:
“3 (1/4 units)”
Operator:
“3/4 of something”
Quotient:
“3 divided by 4”
Ratio:
“3 to 4”

Egyptian Fractions
-Unit fractions meaning 1/n
- breaking larger fractions into smaller parts

Multiplying Fractions

The area model is a visual way to multiply fractions that make it easier to understand than just using the original algorithm.

Dividing Fractions

Number line method:

3/4 divided by 2/3
Step 1. Find common denominator
9/12 divided by 8/12
Step 2. Draw numberline for 12/12

0-----------12/12
Step 3. Specify 9/12 which is what you are dividing from

0--------9/12--12/12
Step 4. Make groups of 8 from the 9/12
0-------8/12 9/12--12/12
Step 5. You could fit one whole group and 1/8 of another so your answer is 1 and 1/8

You can divide fractions by using the area model or the number line model. This video explains the area model in detail and gives you examples.

Divisibility Rules

Divisibility rules help you to easily know if a number is divisible by another without having to do all of the long math like usual. Some rules are easy to follow, like 2 and 5, but other can get confusing.

Properties

Addition and multiplication mostly have the same properties while subtraction and division have similar properties.

Addition:
Commutative- the flip of the equation has the same answer
Associative- the numbers can be put into different groups with parenthesis and still equal the same no matter what
Identity- Anything +0 equals itself

Multiplication:
Closed- an integer multiplied by another integer equals an integer
Commutative- the flip of the equation has the same answer
Associative- the numbers can be put into different groups with parenthesis and still equal the same no matter what
Identity- Any number multiplied by one will equal itself

Subtraction:
Subtraction does not have commutative or associative properties. But it could have an identity property by subtracting 0 from the number and getting itself

Properties of Division

Division can not have commutative or associative properties because it is similar to division in those ways.

- Division does not have commutative or associative properties
- Division have an identity property. If you divide the number by one, it will equal itself

Sets

There are many different ways to express how sets have similarities. Using these sybols allows for it to be simplified.U equals "or" and the reciprocal of that equals "and"

1-1 Correspondence:
There in one input for every one output

Sequences:
Sequences are just like sets in the way that they are a list of elements, but sequences have to be in order
ex: 1, 2, 3. 4

Venn Diagrams are a way to visually represent sets.

Clock/Modular Arithmetic

We are used to only a 12 hour clock, but when using a 24 hour cloch, it help to know how to use clock arithmetic.

Absolute Value

ex. Absolute value of 4 and (-4) are both 4 because its the distnce away from zero.If it was -(absolute value of 4) then the answer would be negative 4 because the (-) is on the outside.

Means the distance away from zero

-| x | = 2 (none)
-| x | = negative (all integers except 0)
-| x | = positive (none)
-x + 1 = positive (x is less than one)

Sequences

A sequence is an ordered list of objects, events, or numbers which may be referred to as elements of a sequence, members of the sequence or terms of the sequence.

Arithmetic:
Sequences of numbers with a common difference. (+,-)
explicit equation= a sub 1 + (n-1)d with d being the common difference

Geometric:
Has a common ratio. (multplication, division)
explicit equation= r to the (n-1) times a sub 1