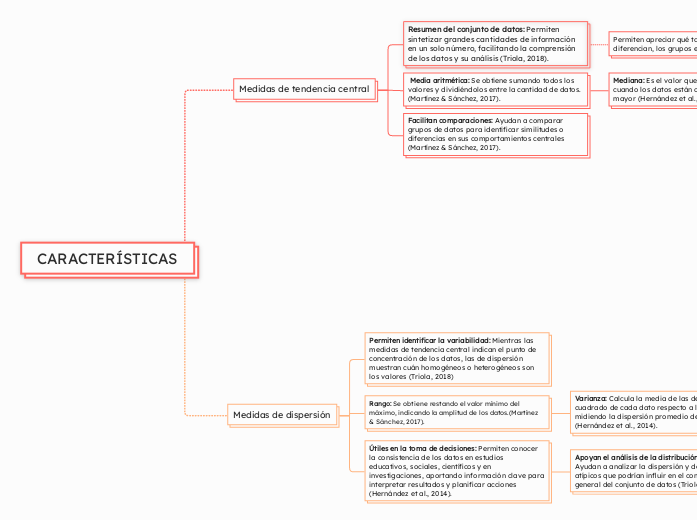
CARACTERÍSTICAS

Medidas de tendencia central

Resumen del conjunto de datos: Permiten sintetizar grandes cantidades de información en un solo número, facilitando la comprensión de los datos y su análisis (Triola, 2018).

Permiten apreciar qué tanto se parecen, o se diferencian, los grupos entre sí.

Son valores que se calculan para un grupo de datos y que se utiliza para describirlos de alguna manera

Media aritmética: Se obtiene sumando todos los valores y dividiéndolos entre la cantidad de datos. (Martínez & Sánchez, 2017).

Mediana: Es el valor que ocupa la posición central cuando los datos están ordenados de menor a mayor (Hernández et al., 2014).

Moda: Es el valor que más se repite en el conjunto de datos. (Triola, 2018).

Facilitan comparaciones: Ayudan a comparar grupos de datos para identificar similitudes o diferencias en sus comportamientos centrales (Martínez & Sánchez, 2017).

Medidas de dispersión

Permiten identificar la variabilidad: Mientras las medidas de tendencia central indican el punto de concentración de los datos, las de dispersión muestran cuán homogéneos o heterogéneos son los valores (Triola, 2018)

Rango: Se obtiene restando el valor mínimo del máximo, indicando la amplitud de los datos.(Martínez & Sánchez, 2017).

Varianza: Calcula la media de las desviaciones al cuadrado de cada dato respecto a la media, midiendo la dispersión promedio de los datos (Hernández et al., 2014).

Desviación estándar: Es la raíz cuadrada de la varianza, expresada en las mismas unidades que los datos (Triola, 2018).

Útiles en la toma de decisiones: Permiten conocer la consistencia de los datos en estudios educativos, sociales, científicos y en investigaciones, aportando información clave para interpretar resultados y planificar acciones (Hernández et al., 2014).

Apoyan el análisis de la distribución de datos: Ayudan a analizar la dispersión y detectar valores atípicos que podrían influir en el comportamiento general del conjunto de datos (Triola, 2018).