Information and Resources about Integers
Absolute Value
Absolute value is also known as the magnitude of an integer.
Absolute Value Problems and Resources
Practice Problems
Addition of Integers
Addition Properties of Integers
Closure Property (m+n is an integer)
Closure and Commutative Properties
Commutative Property (m+n = n+m)

Additive-Identity Property of O (0+m = m+0 = m)
It is also known as the Additive Inverse Property.
Addition of Integers by Using a Number Line

You can add numbers on a number line by simply hopping or jumping from point to point to find the answer.

You can also add a negative number to a positive one using the same technique.
Subtraction of Integers
Subtraction is the "take away" representation of numbers and can be shown using a number line.
If a, b and c are integers, then (a-b = c) if and only if (a = c+b).

Subtracting by adding the opposite: a-b = a+(-b)
Ordering the Set of Integers

If a and b are any two integers, then precisely one of the following relations holds: a is greater than b, a is less than b or a is equal to b.
Number Line Representations
Number lines are represented with zero in the middle, negative numbers to the left of the zero and positive numbers to the right of the zero.

Number Line Example
Multiplication of Integers
1. m(-n) = -mn
2. (-m)n = -mn
3. (-m)(-n) = mn

Closure Property (rs is an integer)

Associative Property (r(st) = (rs)t)
Distributive Property (r(s+t) = rs+rt)

Multiplicative Property of 0 ((0)(r) = (r)(0) = 0)
Multiplication Using a Number Line

6 times 4 equals 24/4 times 6 equals 24
Division of Integers
Fact Families
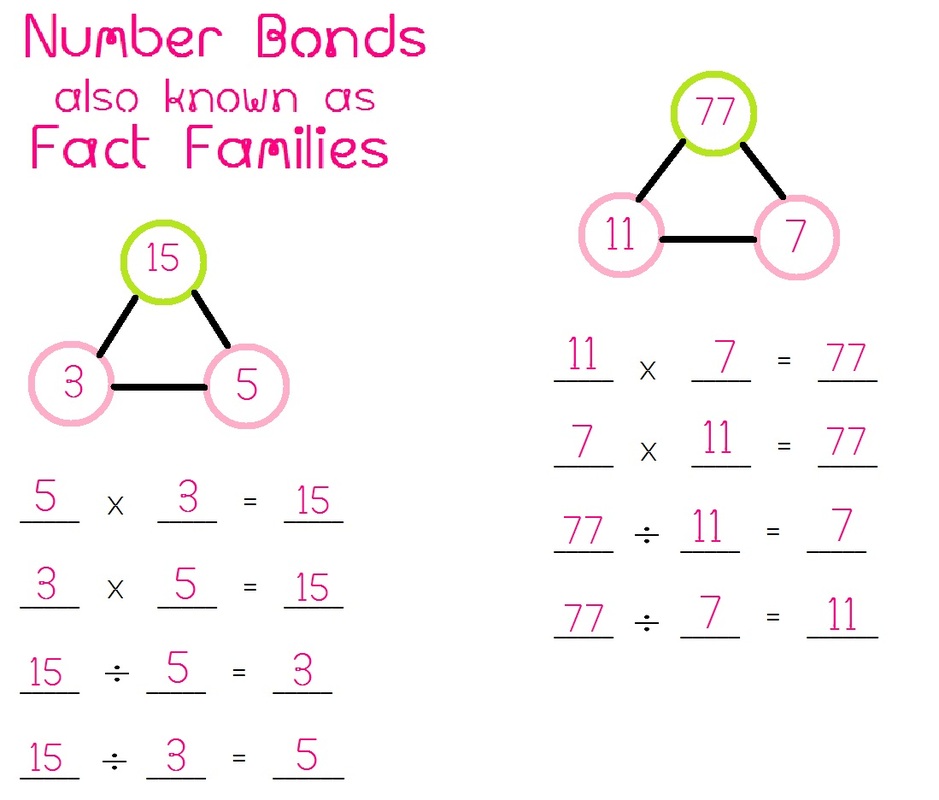
If a, b and c are whole numbers, with b not equal to 0, then a/b = c if and only if a = bc.

The Rule of Signs
Division Sign Practice