CONJUTOS: Es un grupo de elementos claramente definidos
GENERALIDADES
Los elementos se denotan con letras minúsculas: a, b,c .... y se separan con comas: 2,3,4,
Los conjuntos se nombran con letras mayúsculas como: A,B,C ....
Cuando un elemento pertenece a un conjunto se dice que el elemento PERTENECE al conjunto, se denota con el símbolo ∈ y cuando ese elemento NO PERTENECE se denota con el símbolo ∉
Como se enuncian los conjuntos?
POR EXTENSIÓN: Cuando se nombran o listan cada uno de sus elementos y son encerrados entre llaves : {a, e,i,o,u}
N= [2,4,6,8,10]
POR COMPRENSIÓN: Cuando se enuncia una propiedad común a todos los elementos V= { x/x es una vocal}
N= [x/x es un número par menor de 10]
DIAGRAMAS DE VENN: Son figuras que permiten visualizar los elementos de un conjunto, normalmente son circulos u óvalos
Subtopic
DESCRIPCION VERBAL: Cuando se enuncia una característica común a todos los elementos.
N=[ Conjunto de los números pares de uno a 10]
Cuando todos los elementos de un conjunto están contenidos en otro conjunto : se dice que el Conjunto A es Subconjunto de B , e denota A ⊂ B.
Si no todos los elementos de A son elementos del conjunto B , se dice que A no es subconjunto de B .se denota A ⊄ B.
A=[ 0,1,2,3,4,5] B=[ 3,4,5] entonces B ⊂ A C=[ m,a,n,u] D= [ l, o, v , e] entonces C ⊄ D
La cardinalidad de un conjunto es el número de elementos que posee. Se denota por medio
de los símbolos η o # . η(S) = 7
PRODUCTO CARTESIANO DE DOS CONJUNTOS
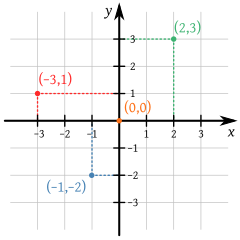
El producto cartesiano de dos conjuntos A y B es el conjunto de todos los posibles pares ordenados que se forman eligiendo como primera componente a un elemento que pertenezca a A , y como segunda
componente a un elemento que pertenezca a B .
El producto cartesiano se denota de la siguiente forma: A× B y se lee “ A cruz B ”.
NOMBRES DE LOS CONJUNTOS
vacío o nulo :No posee elementos. Se denota por: φ o { }.
C= [El conjunto de los caballos de cinco patas]
Universal: Es el que contiene todos los elementos.Se denota por
U. Se representan por un rectangulo
U= [x/x son las Las letra del abecedario]
Iguales: Tienen exactamente los mismos elementos. Se denota por el símbolo = .
M=[Letras del monbre manuela] L=[m.a.n.u.e.l.a]
• Dos conjuntos son desiguales si por lo menos difieren en un elemento, no tienen
exactamente los mismos elementos. Se denota por el símbolo ≠
M= [Municipios del departamento de Cundinamarca] P= [Municipios del departamento de Boyacá]
Dos conjuntos son equivalentes si tienen la misma cantidad de elementos, es decir, si poseen la
misma cardinalidad. Se denota por el símbolo ≈ .
Subtopic
OPERACIONES ENTRE CONJUNTOS
La Unión:n Es la suma de los elementos de dos conjuntos, sin repetir ninguno. A∪ B = { x/ x ∈ A o x/X ∈ B }
A=[1,2,3,4,5] B=[1,3,5,7,9] A∪ B=[ 1,2,3,4,5,7,9]

Subtopic
Subtopic
Subtopic
Subtopic
Subtopic
La interscción: Es el conjunto de los elementos de A que también
pertenecen a B y se denota como A∩ B . Esto es:
A ∩ B = { x x ∈ A y x ∈ B } A=[1,2,3,4,5] B=[1,3,5,7,9] A∩ B=[ 1,3,5]

El complemento Son los elementos que se encuentran en el conjunto A y le hacen faltan al conjunto U para completar todos los elementos. Se denota como 'A . Esto es:
'A = { x ∈U x∉ A} A= [vocales] c= [consonantes] U= [abecedario]

Subtopic
La Diferencia: son elementos que
pertenecen a A y no pertenecen a B y se denota como A− B . Esto es: A − B = { x x ∈ A y x ∉ B }

Subtopic

Subtopic
PROPIEDADES DE LOS CONJUNTOS
jhh
Propiedad de identidad A∪ φ = A
A∪U = U
A∩U = A
A∩φ = φ
Propiedades de idempotencia:
A∪ A = A
A∩ A = A
Propiedades de complemento:
A∪ 'A = U
A∩ 'A = φ
Propiedades asociativas:
(A∪ B)∪C = A∪ (B ∪C)
(A∩ B)∩C = A∩ (B ∩C)
Propiedades conmutativas
A∪ B = B ∪ A
A∩ B = B ∩ A
Propiedades distributivas
A∪ (B ∩C) = (A∪ B)∩(A∪C)
A∩(B ∪C) = (A∩ B)∪(A∩C)
LEYES DE MORGAN
Primera ley. El complemento de la unión de dos conjuntos es la intersección de sus complemeto (A∪ B)' = 'A ∩ 'B
Segunda ley: El complemento de la intersección de dos conjuntos es la unión de sus complementos:
(A ∩ B)' = 'A ∪ 'B

