Elementary Mathematics
Week 1
Syllabus week
Week 2
Converting bases
Converting bases using diagramsTo convert from other bases to base 10 you would start off by drawing your diagram with however many longs, flats and units you haveexample: convert 12 base seven to base 10You would start by drawing one long and two unitsSince you are in base seven, the long would have 7 in it Next you would add your units which would be 27+2= 9
Other bases
Adding in other bases
Adding in other basesYou would draw out your diagram with how many flats, longs and units you have for each number and put plus sign in the middle then add but keep in mind your base in case you have the number of units for the base which then would make a long and so onexample: add 13 and 31 base fiveFor 13 you would draw 1 long and 3 unitsFor 31 you would draw three longs and one unitsStart by adding the longs so 1+3= 4 longsNow add the units which 3+1= 4 unitsSo we get 44 units in base five
Algorithms for converting bases
Converting to other bases
Converting to other basesYou can use the method of upside down division in which your final answer will be written from the left up to the right Put the base your converting to on the outside left and the number you are converting inside an upside down division simpleDivide as normal but put your remainders on the right side outside the boxAnother option: You may draw a diagram by skip counting by your base
Convert to base ten
Convert from other bases to base tenUse algorithmexample: convert 34 base seven to base tenYou would start with a three then put seven inside your parentheses since it is your base and raise it to the first power because you have two numbersNow add 4 with seven (the base) inside the parentheses and raise it to the 0 3(7^1)+4(7^0) Now solve 3(7)+4= 25
Week 4
Alternative Algorithms for Adding
Expanded form
Adding using Expanded formBreak down the numbers based off of place valueThen line up the numbers vertically and addAdd the answers you got horizontally to get your final answerExample: Add 258 and 387200 + 50 + 8300 + 80 +7___________500+130+15 = 645
Left to right
Left to right Set up problem verticallyAdd numbers in the same place value one at a timeThen add together the numbers you got for each place valueExample: Add 428+294 428+294--------60011012------722
Friendly numbers
Adding using friendly numbersThe goal is to turn as many numbers into 10's (or multiples of 10) which will be easier to add which you do by borrowing from other numbers to get your number to end in a 0Example57+ 28 + 16 +34 + 62 +43 +16You can take away 3 from 43 and give it to 57 to make 60Take away 2 from 62 and give it to 28 to make 30Take away 4 from 34 and give it to 16 to make 20Now add together all the numbers60+40+60+30+30+20+16 = 256
Scratch Method
Scratch methodAdd numbers up in each column until you reach 10 then you will make a slash through the number and write down any remainders by it and keep goingAt the end of the column write your remainder if anyCount up the number of slash marks in the row and add it to the top of the next rowRepeat process
Trade off
Add using trade offThe goal is to make numbers easier to add numbers such as numbers that are multiples of 10, 5, etc. by trading off with other numbers and replacing the valueex: 34 + 57 + 66 + 92 + 20 + 33You can take away 4 from 34 and add it to 66 to make 70You can take away 2 from 90 and trade it off to 33 to make 35Add together all the numbers including the new ones30+ 70+ 90+ 35+ 57+ 20= 302
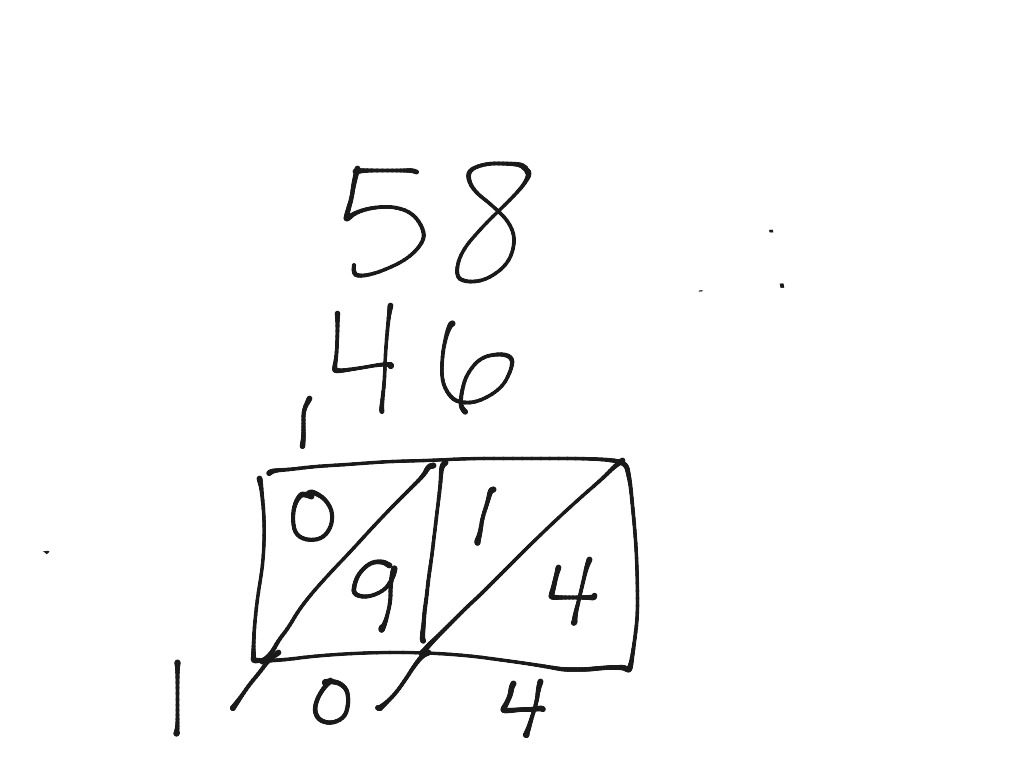
Lattice
Lattice Set up the problem as usual then under it draw enough boxes so if double digit two boxes and draw a diagonal line in themAdd as usual and add up the numbers on each diagonal line at the end
Week 5
Alternative Algorithms for multiplying
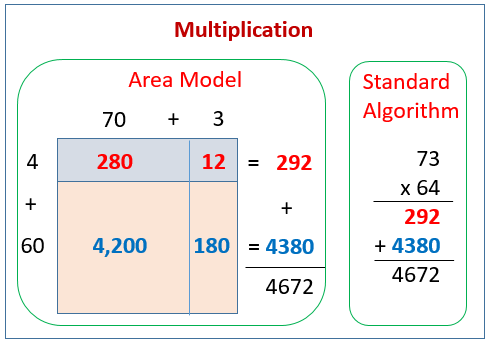
Area Model
Multiplying using area modelBegin by drawing a rectangle and breaking down the numbers you are multiplying by putting them in expanded form and a plus sign in between on the left of the rectangle and the top example: 21(14) would be 20+1 and then on the top line 10+4Where you have a plus sign draw a line Then multiply the numbers on the left by the numbers on the top line and fill in each square
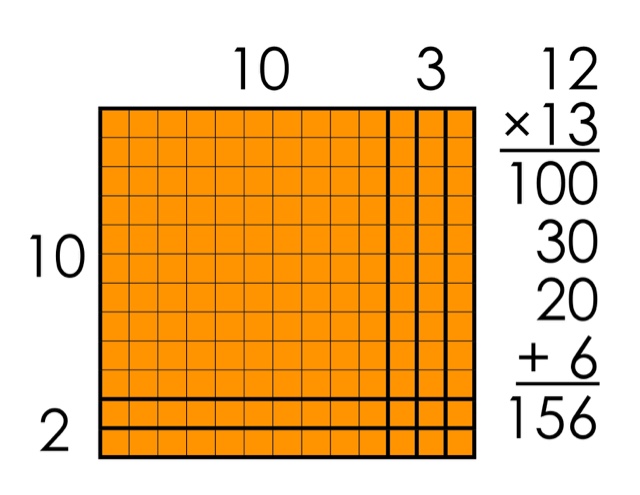
Base 10 model
Base 10 modelDraw out numbers as you would if you were setting it up with base 10 blocks Break down first number you are using on the left then the other on the topAT the end count everything up
Groups
Multiply using groupsExample: 2(3)We have two groups of three which can be drawn out by having two circles that each have threeOnce the circles are drawn out we count how much we have in each circle and add it up so we would have 6
Week 6
Review/Exam
Week 7
Multiplication Alternative Algorithms
Array
Multiply using arraysThe first number indicates how much will be in each column and the second number is how many columns to drawAdd up all of them to get answerex: 3(4) . . . . . . . . . . . . =12Can also be done by drawing horizontal and vertical lines (how many depending on problem)ex: 3(4) would be 3 horizontal lines and 4 vertical to equal 12
Expanded form
Multiply using expanded formStart off by breaking down numbers into expanded form then set up as a normal multiplication problemAlways start multiplying at the left row (40x20) and (40x3)Move onto the next row and multiply (5x20) and (5x3)Make sure when writing the answers to keep the addition sign in betweenAt the end add up all numbersex: 23(45) 20 + 3x 40 + 5 ------------- 800 + 120+100 +15--------------900 + 135 = 1035
Lattice
Lattice (Multiplication)Depending on the number draw the appropriate amount of boxes (2 digit: 2 columns and 2 rows) (3 digit: 3 columns and 3 rows)Similar to lattice in addition draw a diagonal line through each boxStart multiplying and fill the answers in each boxAdd up the numbers following the diagonal lineWhen there is 10 or you reach the number in your base add the extra number to the next lineEx: 47(68)You would multiply 4(6) in the first box and 7(6) in the secondIn the next row you would multiply 4(8) and 7(8) in each of the boxesAdd up the numbers at the end of each of the diagonal sections Answer: 3196
Alternative Algorithms for division
Repeated subtraction
Repeated subtractionSet up similar to traditional division except it has a line going down on the right sideThe goal is to estimate with numbers students know so they can work with numbers that are easier for themThe numbers on the right should be added up to get your answer and the left side will be the remainderex: 523 divided by 42.. ___42| 523 |..........-420 | 10.....------ |..........103 | 1........-42 |......------ |............61 | 1........-42 |..................----- | + -----........................19 | 12 19/42Answer: 12 and 19/42
Upwards division
Upwards divisionSet up problem as it is said (47 over 7)Multiply as usual (6x7 is closest to 47 so write 6 after the = and subtract what is left from 47 on the left side)Since there is 5 left over and the denominator is 7 it will be a remainder of 5/7ex: 47 divided by 747-42=5--- = 67Answer: 6 and 5/7
Alternative Algorithms for subtraction
Show using diagram
Show (subtraction)Start by drawing your number (all the ones, tens and so on)Then circle the amount you are taking away with an arrow and you will be left with your answerex: 6-2You would draw six units and take away 2 by circling them and drawing an arrow at the end to show you are taking awayYou would be left with 4 which is your answer
Equal Addend
Equal AddendUsed to avoid borrowingchange to easier numbers to work withex: 43-19Can change 43 to 44, since I added 1 I do the same to the other number43+1= 4419+1= 20Now we have 44-20.44-20-----.24
Week 11
Divisibility Rules
Divisibility Rules (useful for finding factors)2: Even numbers (ends in 2,4,6,8,0) ex: 723: Sum of digits is divisible by 3 ex: 4324: Last two digits are divisible by 4 ex: 35125: Any number ending in a 5 or a 0. ex: 34656: Even and sum of digits is divisible by 3 ex: 5288: Last three digits are divisible by 8 ex: 52089: Sum of digits is divisible by 9 ex: 437410: Any number ending in zero ex: 250
Prime Factorization
Prime factorization ..40. ../\10...4/\..../\5 2 2 2Factor until you reach a prime number then once you do your bottom row is your answerP.F: 23 . 5ex: 30 (using upside down division)3|30_2|10_...5P.F: 2.3.5
Algorithm for multiplying fractions
Multiplying fractions algorithm ex: 8/10 x 3/4Break down numbers into their factors8 into 2x4, 10 into 2x53 stays the same and so does 4Wherever you see the same number on the numerator and denominator draw a large one "funky one" connecting themso draw a funky one connecting two and two on the left fractionDraw a funky one diagonally connecting the two 4'sNow circle the numbers that don't have funky onesMultiply the numbers that are left straight across (the circled ones)So we get 3 on the top and 5 on the bottomAnswer: 3/5When you have a mixed number draw a "backwards" C and multiply the left number with the denominator then add the numeratorThen continue on with the same process from the example above
Week 10
Multiply Fractions
Multiply fractions (Build)ex: 3(5) = 3 groups of 5Draw 3 groups of 5 and count them all up to get 15ex: 1/2 (1/4) = half a group of 1/4Would draw a group with 1/4 (could be of a circle) and split it in halfex: 1/2 (4) = half a group of 4Draw a group with four and divide it in half (to get 2)
Algorithms for adding fractions
Adding fractions ex: 4 + 2/7 can add straight across = 4 2/7ex: 5 3/7 + 4 1/7Start off by adding whole numbers 5+4=9Then add fractions 3/7 +1/7 = 5/7Combine to get 9 5/7ex: 3/10 + 5/12break down the denominators into their factors (10 into 5x2) (12 into 6 x2)Multiply by what is missing to get common denominatorsFor the first fraction you'd multiply by 6 on top and bottom (6/6)For the second you would multiply by 5 on top and bottom (5/5)you get 18/60 and 25/60 so add together to get final answerAnswer: 43/60
Algorithms for subtracting fractions
Subtracting fractionsex: 12- 1/4"Borrow" from the twelve by turning it into 11 4/4Now subtract the fractions 4/4 -1/4= 3/4Answer: 11 3/4ex: 2/3 - 4/9Break down each fraction's denominators into factors (the first is already done)For the second fraction would be (3x3)Multiply by what is missing (the first is missing a 3 so multiply by 3/3)Now you have 6/9 - 4/9 = 2/9
Week 9
Intro to fractions
Intro to fractionsFractions are a comparison The numerator = the number of piecesThe denominator = the size of the piecesModelsLinear model: compares length, how long a part is compared to the whole ex: 5/7 of the squares are blue Set model: Total number out of whole set (comparing certain amount of items to the total number of items)ex: 4/6 are pink ex: 3/5 are circlesArea model: compares area (usually is a circle or rectangle)ex: 1/3 of the area is blue ex: 1/4 of the area is red
Add fractions (show)
Add fractions using diagramex: 1/3 + 1/4Draw a rectangle divided into 3 sections and fill one inDraw a rectangle next to it with 4 sections and fill one in Now on each rectangle divide it into the sections for the opposite rectangle (divide the first rectangle into 4 sections going the opposite way) (divide the section rectangle into 3 sections going the opposite way)Draw a third rectangle underneath, divide into the same sections as above (so 12 squares)Now add up the shaded squares from each of the rectangles above and shade them into the new rectangle4 shaded squares from the first and 3 from the second4+3= 7The total number of shaded squares is your answer with the total number of squares as your denominatorAnswer: 7/12
Subtract fractions (show)
Subtract fractions using a diagramex: 3/4 - 1/3Draw a rectangle for the first fraction (divided into 4 sections, 3 of them are shaded)Draw a second rectangle for the next fraction (3 sections with one of them shaded)Now on each rectangle divide it into the sections for the opposite rectangle (3 sections going in the opposite direction for the first) (4 sections going in the opposite direction for the second)Since we are subtracting 1/3 we want to put an X on one third of the boxes to remove itFor the second rectangle we X out all that is shaded (since its 1/3)In the first rectangle we X out 4 boxes (since from the previous box we saw 1/3 is 4 boxes)Now we count of the number of boxes that are shadedWe have 5 still shaded and the total number of boxes is 12 which is the denominator So the answer is 5/12

Multiply fractions (show)
Multiply fractions using diagramsex: (2/3) (1/2)Draw a rectangle and draw the appropriate number of sections per each fractionSplit into 3 sections and shade 2 of them then in the other direction split in two sections and shade oneThe area that is double shaded will be the answer2 boxes are double shaded and 6 is the total number of boxes so the answer is 2/6
Week 8
Intro to integers
Integers (Show)Always put positives on top, represented by +Negatives go on the bottom, represented by -Zero bank: a positive and negative together which makes zero (circle it)ex: Show 2 using 6 tiles++++--ex: show -6 + 4++++------ = -2
Add integers
Add integersThe bigger pile gets two signs above the number (sign depends if it is negative or positive)The other gets one sign above the number (depends if its positive or negative)Circle the single sign and one of the signs from the double pileSame sign = add, different sign= subtractThe sign not circled will be the sign of the answerex: -39 + 10Since -39 is bigger it would have two --10 would have +Circle the signs, which are different so subtract39-10= 29The left over sign is - so the answer is -29
Subtract Integers
Subtract integersUse keep, change, change (the signs)Use the same method for additionex: -25 - (-15)Keep change change would give us -25+15-25 is bigger pile so it gets two --15 gets +Circle signs, they are different so subtract25-15= 10The left over sign is negative so the answer is -10
Multiply Integers
Multiply integers (show)ex: 3(4)The first number is the number of groups, the second is how much is in each groupWould be three groups of fourAdd up all of the circles to get your answer, = 12++ ++ ++++ ++ + +ex: -2(-3)Take away 2 groups of 3 negatives+++ +++--- --- All that would be left is the positives so the answer is 6
