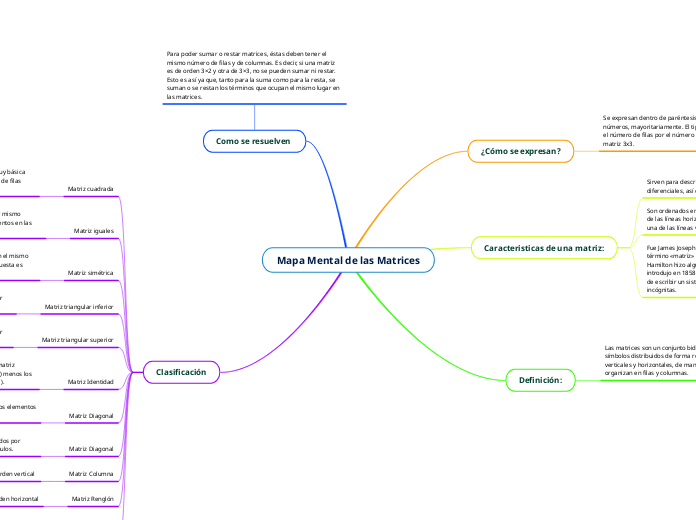
Mapa Mental de las Matrices

Se expresan dentro de paréntesis y en el interior encontramos números, mayoritariamente. El tipo de matriz, se expresa con el número de filas por el número de columnas. Por ejemplo: matriz 3x3.

Sirven para describir sistemas de ecuaciones lineales o diferenciales, así como para representar una aplicación lineal.

Son ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales.

Fue James Joseph Sylvester quien utilizó por primera vez el término «matriz» en 1848/1850. En 1853, William Rowan Hamilton hizo algunos aportes a la teoría de matrices. Cayley introdujo en 1858 la notación matricial, como forma abreviada de escribir un sistema de m ecuaciones lineales con n incógnitas.

Las matrices son un conjunto bidimensional de números o símbolos distribuidos de forma rectangular, en líneas verticales y horizontales, de manera que sus elementos se organizan en filas y columnas.

Para poder sumar o restar matrices, éstas deben tener el mismo número de filas y de columnas. Es decir, si una matriz es de orden 3×2 y otra de 3×3, no se pueden sumar ni restar. Esto es así ya que, tanto para la suma como para la resta, se suman o se restan los términos que ocupan el mismo lugar en las matrices.

Matriz cuadrada

Una matriz cuadrada es una tipología de matriz muy básica que se caracteriza por tener el mismo orden tanto de filas como de columnas.

Matriz iguales

Se dice que dos matrices son iguales si tienen el mismo tamaño (dimensión u orden) y los mismos elementos en las mismas posiciones.

Matriz simétrica

Una matriz simétrica es una matriz de orden n con el mismo número de filas y columnas donde su matriz traspuesta es igual a la matriz original.

Matriz triangular inferior

En una matriz triangular inferior los elementos situados por encima de la diagonal principal son ceros.

Matriz triangular superior

En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros

Matriz Identidad

Una matriz identidad o unidad de orden n es una matriz cuadrada donde todos sus elementos son ceros (0) menos los elementos de la diagonal principal que son unos (1).

Matriz Diagonal

Una matriz A=(aij) A = ( a i j ) es diagonal cuando los elementos que no están en la diagonal son 0

Matriz Diagonal

En una matriz diagonal todos los elementos situados por encima y por debajo de la diagonal principal son nulos.

Matriz Columna

Es aquella en orden vertical

Matriz Renglón

Es aquella en orden horizontal

Matriz Cero

En una matriz nula todos los elementos son ceros. En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.