Math - Understanding Integer Operations and Properties
The goal of this Mind Map is to introduce the concept of integers and how they are used in the classroom. I will provide online tutorials, games and links to resources that may be used in the elementary math classroom.I am including information in this map from "Mathematics for Elementary School Teachers", O'daffer, Charles, Cooney, Dssey, Schielack, Pearson Education, 2008.
Addition, Subtraction, and Order Properties of Integers
The set of inegers, I, consists of the positive integers (i.e., the nonzero whole numbers), the negative integers, and zero. For example:I={...-3,-2,-1,0,1,2,3)
Integers
A set of integers is made up of the positive integers , the negative integers, and zero.I = {...-3,-2,-1,0,1,2,3}

Adding Integers
Basic Properties of Integer Addition
1. Additive Inverse Property
Additive Inverse PropertyFor each integer a, there is a specific integer -a that verifies the formula of a + (-a) = 0For example, if you substitute 4 in for integer a:4 + (-4) = 0
2. Closure Property
Closure PropertyFor all integers a and b, a + b results in a specific numberGiven: a = 6 and b = 7 6 + 7 = 13
3. Additive Identity Propery
Additive Identity PropertyThe sum of any number, a, and zero yields the original number, a.For example:a + 0 = aIf a is 3:3 + 0 = 3
4. Commutative Property
Commutative PropertyWhen two numbers are added, the sum is the same regardless of the order in which they are added together.For all integers a and b, a + b = b + aFor example: a = 3, b = 23 + 2 = 2 +35 = 5
5. Associative Property
Associative PropertyThe sum of two numbers added with a third number is equal to the sum of each number added with the third number in the set. It doesn't matter what order you add them in or whether they are in parenthesis, the answer will always come out the same.For numbers a, b, and c, (a + b) + c = a + (b + c)For example, a=2, b=1, and c=4(2+1) + 4 = 2 + (1 + 4)3 + 4 = 2 + 57 = 7
Subtracting Integers
Subtracting Integers is essentially the "opposite" of adding them. One can swap out the numbers in an equation to work towards the answer they need. You can subtract an integer by simply adding its opposite value.For instance:If a-b=c if and only if c+b=aYou can put the example together of a=5, b=2, c=?5-2=3 double check by proving 3+2=5
aSubtracting Song

Less Than (<) and Greater Than (>)
Explanation of less than (<) and greater than (>) for integers:a < b if and only if there is a positive integer p such that a + p = b. Which also means that b > a only if a < b, you simply reverse the sign and numbers.For example:a = 1, p=3, and b = 41<4 if 1 + 3= 44>1 only if 1<4
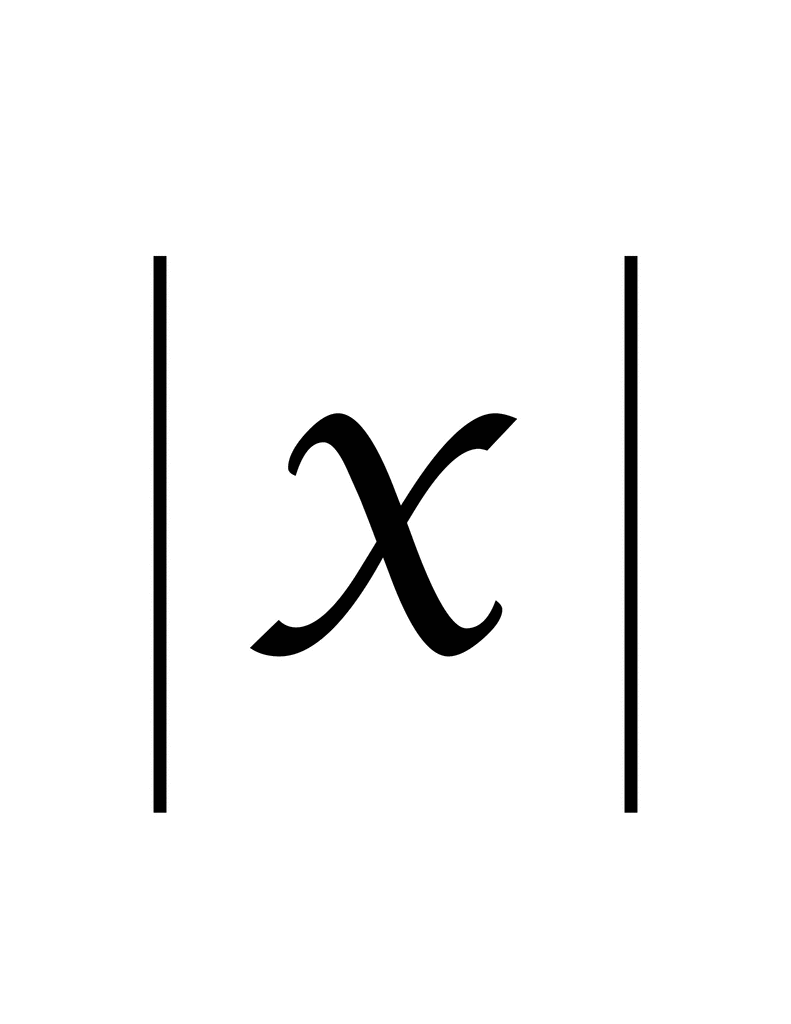
Absolute Value
The definition of the absolute value of an integer is the distance the number is from zero. Whether the number is -8 or +8, both integers are 8 units away from zero. The absolute value of n is written |n| and is positive for all n not equal to zero. |n| = n, if n is positive or zero. |n| = -n, if n is negativeFor example The absolute value of |-8| = 8The absolute value of |8| = 8
Dividing Integers

Dividing Integers
Dividing numbers or integers can be thought of as splitting things into equal parts or groups of items.You can prove that the division is accurate by reversing some of the integers into a multiplication problem.For example:a/b=c if we substitute a=6, b=3, c=?6/3 = 2We can check this by multiplying:c x b=a 2 x 3 = 6In our example, a (or 6) is called the dividend, b (or 3) is the divisor, and c (or 2) is the quotient.We can use a real world example of sharing a pizza. There are 8 slices in the pizza and 4 people want to equally share the pizza.8/4 = 2 pieces of pizza for each person
Properties of Integer Division
There are certain rules about division that are important to remember.1) An important property is that you cannot divide an integer/number by 0 because there is not a specific answer/quotient. (ex.cannot use a/0, no answer available)0 divided by a number is always 0. (ex. 0/a=0)2) Another property is that any number divided by itself will always result in the answer/quotient of 1.Ex. 5/5=1, 3/3=1, 200/200=13) The following property is also important:(axb)/a=bThe repeated numbers, a in the example above, cancel each other out and result in only 1 number being left. (b)(4x2)/48/4=2
Dividing Positive/Negative Integers
When you divide positive+ or negative - integers:If you divide two integers with the same signs, the result is always positive. This is sometimes hard for students to understand that two negative numbers can result in a positive answer.Positive ÷ positive = positiveNegative ÷ negative = positiveWhen you divide two integers with different signs, the result is always negative. Positive ÷ negative = negativeNegative ÷ positive = negative
aVideo Example
This is a straight forward video that explains real examples of how the positive and negative integers affect what the answer will be.
Multiplication of Integers
Multiplying Integers
Multiplication is essentially repeated addition. The answer you obtain by multiplying two or more numbers is called the product. You can think of each number as groups with a certain amount in each group. For instance, you might have 2 groups of 3 tennis balls. The following examples show the different ways of thinking about the problem.(1+1+1) + (1+1+1) = 63+3 = 63x2 = 6
a1. Closure Property
Closure PropertyFor all integers a and b, ab results in a specific numberGiven: a = 2 and b = 3 2 x 3 = 6
2. Multiplication Identity Property
Multiplication Identity Property1 is the only specific integer that for each number a, a x 1 = 1 x a = a.This can be shown by using multiple different examples and the answer still remains that the original number is the product.2 x 1 = 1 x 2 = 25 x 1 = 1 x 5 = 5100 x 1 = 1 x 100 = 100
3. Commutative Property
Commutative PropertyFor all numbers, the order in which you multiply does not change the product (answer). You can switch the order the multiplication problem is presented and still have the same answer.For example:2x4=4x28=8
4. Associative Property
Associative PropertyWhen three or more numbers are multiplied together in a problem, the product is the same regardless of the way the numbers are arranged. For example:(2x3)x4=2x(3x4)(6)x4=2x(12)24=24
5. Distributive Property
6. Zero Property
Zero Property for Multiplication
Multiplying Positive/Negative Integers
When you multiply positive+ or negative - integers:If you multiply two integers with the same signs, the result is always positive. This is sometimes hard for students to understand that two negative numbers can result in a positive answer.Positive x positive = positiveNegative x negative = positiveWhen you multiply two integers with opposite signs, the result is always negative.Positive x negative = negativeNegative x positive = negative1. Two positives you get a positive:+ x + = +2. Positive and a negative you get a negative:+ x - = -3. Negative and a positive you get a negative:- x + = -4. Two negatives you get a positive:- x - = +