Statistics

Variables

Response variable

Value depends on explanatory variable

Plotted on the y axis

Explanatory variables

Explains the change in the variable and affects the value of the response variable

Plotted on the x axis

Scatterplot

Scatterplots ae used to study the relationship between 2 quantitative variables

The variables are plotted and the relationship is noted

Relationship

Negative

Smaller variables of one variable is associated with the smaller value of the other variable

Positive

Larger values of one variable is associated with the larger values of the other variable

Points to note

Direction

Overall direction of relationship

Strength

Strength of relationship

Outliers

Outliers must be noted

Correation

Denoted by r

Helps to measure the strength and direction of a relationship between 2 variables

If r > 0 relationship is positive and if r < 0 relationship is negative

If r is near 0 , might mean no relation ship or a strong non linear relationship , if r is close to 1 or -1 then the relationship is linear

-1≤r≤1

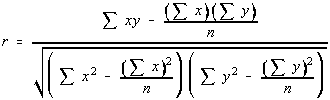
r is not a resistant measure

Regression Line

A line drawn through a scatter plot so that it is close to as many points as possible

Least Squares Regression Line

The line that minimizes the sum of the squre of the differences between the observed values and values predicted by the line

y= a + bx

Can be used to predict values

Residuals

Observed Y - Predicted Y

Sum of residuals is 0

Mean of redisuals is 0

Plot of residuals

Plot of residuals must have no pattern

If there is a pattern in the residual plot

It means that a non linear relationship would better explain the data

Coefficent of determination

Denoted by r^2

Gives the percentage of data that can be explained by the regression line

Cautions

Outliers

Shows up as a point with a very large residual

Lurking variables

May affect the relationship between variables without being aparent

Measuring the Center

Mean

Sum of all the elements of a set divided by the number of elements

Can be affected by outliers

Median

The middle value of a data set once it has been arranged ascendingly or descendingly

Resistant to outliers

Meauring the Spread

Range

Interquartile Range

The difference between the largest and smallest value

IQR can be used to remove influence of extreme values

It is the middle 50% of the data ( i.e that the bottom and top 25% have been removed

Outliers

Values more than 1.5(IQR) below the 1st quartile of more than the 3rd quartile are outliers

Variance

Average of the squared deviations from the mean

Standard Deviation

Gives a measure of spread around the sample mean

Affected by outliers , use only mean is also used

n-1 is the degrees of freedom

Boxplots are very useful

Can give the IQR , Median and Outliers

Plotted to check for outliers usually

Modified boxplot is boxplot with outliers removed

Measuring the Position

Simple Ranking

Arranging the elements in some order and noting where in that order a particular value falls

Percentile Ranking

Rank of 80% means that 80% of all values fall below that point or on it

The value at which p% of values fall below or on that point

Quartile ranking in which the data is split into 4 equal quartiles of 25%

Z-Score

The number of standard deviations a values lies from the mean

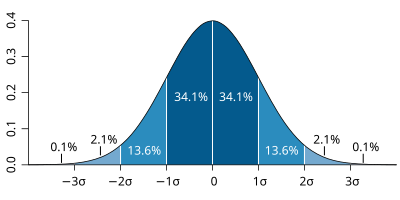
Emperical Rule

a.ka 68-95-99.7 rule

68 % of data lies within 1 standard deviation of the mean

95% of the data lies within 2 standard deviations of the mean

99.7% of the data lies within 3 standard deviations of the mean

Usefull to estimate the standard deviation if we know the data

Quantitative Data

Histogram

A plot of the observation on the x axis and the frequency on the y axis

Suitable for large quantities of data

Easy to visualize data

Total count of data is given by the sum of frequencies

Cummilative frequency plot

Somewhat similar to a histogram

The relative frequency of the data is summed and plotted

Stemplot

Similar to a histogram but the frequency is represented by leafs on a stem

Good to spot normality

Sometimes the plot may get too big

Trim the stemplot

Split the stem into 2

Very important to indicate legend

Catergorical Data

Pie Charts

Each slice of the pie represents the proportion of a particular category

Very good for comparing the proportions of different categories

Bar Chart

Each bar represents a particular category

The height of the bar represents the amount of that category

Important to have the width the same

Dot Plots

Each catergory is plotted on one side and the frequency or value is indicated with dots on the other side of graph

Important to state the legend

Shapes of Graphs

Uniform Distribution

Uniform if the histogram of the distribution is a straight line

Example would be of a dice , the freq for all numbers is 1/6

Skewed graphs

Skewed right

Skewed right if spreads far and thinly towards the higher values

Skewed left

Skewed left is it spreads far and thinly towards the lower values

Symmetric Distribution

2 halves of the graphs are mirror images

Bell shaped curve

If the distribution is symmetric with 2 sloping tails

Describing Graphs

Center

The point that seperates the values(area of graph) roughly in half

Spread

Scope of values from smallest to lagest

Clusters

Natural subgroups that the values fall into

Gaps

Holes in distributions where no values fall in

Outliers

Extreme values of a graph

Usually determined by the 1.5IQR rule

Modes

Unimodal

Only has one peak

Bimodal / Multimodal

Has more than one peaks

Highest peaks in the grpahs

Types of sampling

Bias

Bias is created when the results have a factor that has affected the outcome

Nonresponse

Occurs in convinience sampling usually , when the individaul does not respon to the survey

Small sample size

Small sample size would not give accurate resulkts

Undercoverage

Some people might have been left out in the sample

Different Sampling Types

Random Sampling

SRS ( Simple random sampling)

A random sample size is chosen from a population

Random table can be used to select

Stratifed Sampling

Population is split into different stratas before data is taken from each strata is taken

Usually split into diffeent strata based on common characteristic

Clusters

The population is split into clusters

A particular cluster is chosen and all those in it are included

Voluntary Sampling

Only results of those who respond is considered.

Biased as those who respond may share common trait

Convinience Sampling

Only those who approach the surveyor get sampled

Biased

Census

A census is when the data of the entire population is obtained

Experimental design

Observational Study

Done by observing the outcomes without influencing the enivronment

Experimental Study

Done by altering the environment and observing the results

Degin Types

Matched Pair

Subjects are paired

Each one is put through a different treatment group

Results are compared

Blocked

Subjects with similar conditions that may affect results are blocked

Randomised

Subjects are allocated at random

Blinding

Blinging is important as either party in the experiment knowing anything about the subjects might induce bias

Single blind

The subjects do not know what they are gettting

Double Blind

Both the subjects and the researchers do not know what they are getting

Placebo

Used when comparing 2 treatments, the placebo is a fasle treatement

Used to remove any phsycological bias

Steps to design

Suitable desgin type

Suitable treatments

All variables taken into account

Control

One group may receive the treatment while another control group may not receive any for control purposes

Replication

Experiment needs to be replicated to ensure consisten results

Also helps to remove error brought about by chance

Permutations

Different number of ways a set of objects can be arranged

take note that the order has to be distinct , order matters

n! gives number of ways for n objects to be arranged

(n-1)! gives the number of ways for n objects to be arranged in a circle

When choosing way to arrenge r objects from n

Combinations

Order is ignored

Only number of ways to get different items matters

Objects have to be distinct

Probability

Probability of event

P(x) = 1 means that the event will defenitely and always occur

P(x) = 0 means that the event would not occur

If A and B are disjoint

P(A U B) = P(A) + P(B)

P(A intersect B) = 0

Hypothesis

Null hypo : Nothing is different

Alternative hypo : Different from null

Errors

Type 1 error

Rejecting the null hypothesis when it is true

Type 2 error

Fail to reject null hypothesis when it is not true

Power of test

To increase power

Increase alpha

More extreme alternative

Descrease std deviation

Increase sample size

80% power is used as standard

2 Population

2 Sample Z test

2 Sample T test

Confidence interval

Conservative approach for df

df = Min( n-1 , n02)

Conditions

SRS

Independence

Population size is at least 10(n)

Normality

At least 5 for each sample

n1+n2<15

Normal no outliers and no strong skew

15<n1+n2<30

No outliers and no skewedness must be present in the data

n1+n2>30

Can be used even if distribution is skewed

Hypothesis testing

Degrees of freedom

Conservative

The degrees of freedon of both the samples must be considered and the smaller one chosen

Close approximation

Population Proportion

2 population z-test for hypo. test

Combined sample proportion

Conditions

SRS

Data must be obtained from an srs

Independence

Population size is at least 10 times of sample

Normality

The count of success and failures is at least 5

2 population z-interval for confidence

Conditions

SRS

Data must be obtained from an srs

Independence

Population size is at least 10 times of sample

Normality

The count of success and failures is at least 5

1 Population

Test about population mean

Std deviation known

1 Population Z test

Alternate Hypothesis

Condition

SRS

Data must be obtained from an SRS

Independence

Population is at least 10 times bigger than sample

Normality

Sample size at least 30

Std deviation not known

1 Population T test

Conditions

SRS

Sample must be by SRS

Independence

Populaiton is at least 10 times bigger than sample

Normality

n < 15

Population must be normally distributed and there must be no outliers

n < 30

No outliers or strong skew must be present

n >30

T procedure can be applied even if there is skewedness present in the data

Test about population proportion

Hypothesis

Conditions

SRS

Data must be from an srs

Normality

np and nq must be greater than 10

Independence

Population is 10 times of sample size

Chi Sqaure

Goodness of fit

Each expected cout must be more than 5

2 way table

Null hypothesis

The distribution in the response variable is the same in all x populations

Alternative hypothesis

The x distributions are all not the same

Chi Square distribution

Probability Density Function

Cummilative Distribution Function

Normal

Z score

Gives the number of std deviations the value is from the mean

Usually used for large sample sizes

Generally used for distributions where majority of the obervations cluser around mean

Clear link between mean and standard deviation

Central limit theorem

When the sample size is more than 30

Normality can be assumed

Does not work with proportions

Can be used to approximate binomial and poisson distribution

Bionomial

Conditions

There are only 2 outcomes in the trial, one defined as "Success" and the other as "Failure"

The number of trials n is fixed

The outcome of each trial is independent

Probability of succes for each trial is the same

X~B(n,p)

Mean = np

Std deviation = root(np(1-p))

Normal approximation

Can be approximated to normal distibution

Condition

np and np(1-p) greater than 10

Most accurate when p = 0.5

If p is not close to 0.5 , approximation would be poor

Continuity correction must be performed

Poisson

Conditions

Events occur singly and randomly

Events occur uniformly

Probability of even occuring is very low

Events occur independently

Po(x) + Po(y) = Po(x+y)

Normal approximation

X~ N(np)

np must be large > 50

More accurate if n is large and p very low

Geometric

Conditions

There are only 2 outcomes in the trial, one defined as "success" and the other as "Failure"

The number of trials n is not fixed

The outcome of each trial is independent

Probability of succes for each trial is the same

The variable of interest X is the number of trials before the first succes

mean is 1/p

Standard deviation is q/p^2

Parameter and statistic

Parameter describes a property of a population such as mean

Statistic is usually computated from the sample of a proportion

Samling variablity

Value of statistics varies over many trials

A larger sample would produce lesser variablity

Sampling distribution

Overall shape should be roughly normal

Acceptable if it is skewed but must not have outliers

No outliers should be rpesent

Center of distribution should be close to mean of population

Bias

How far the mean of the sample is from the mean of the population

Sample proportion

Used when meauring the proportion of a population

Mean proportion of sample is equal to that of the population

Standard deviation

Sample mean

Mean of samle is mean of population

Std deviation