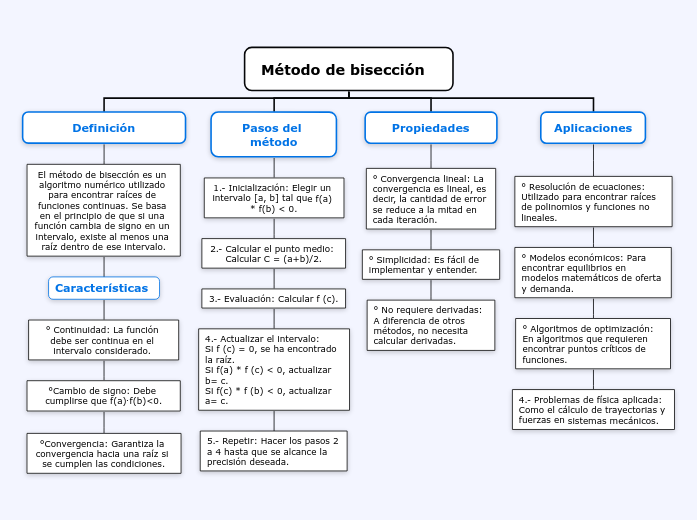
Método de bisección

El método de bisección es un algoritmo numérico utilizado para encontrar raíces de funciones continuas. Se basa en el principio de que si una función cambia de signo en un intervalo, existe al menos una raíz dentro de ese intervalo.

° Continuidad: La función debe ser continua en el intervalo considerado.

°Cambio de signo: Debe cumplirse que f(a)⋅f(b)<0.

°Convergencia: Garantiza la convergencia hacia una raíz si se cumplen las condiciones.

1.- Inicialización: Elegir un intervalo [a, b] tal que f(a) * f(b) < 0.

2.- Calcular el punto medio: Calcular C = (a+b)/2.

3.- Evaluación: Calcular f (c).

4.- Actualizar el intervalo:
Si f (c) = 0, se ha encontrado la raíz.
Si f(a) * f (c) < 0, actualizar b= c.
Si f(c) * f (b) < 0, actualizar a= c.

5.- Repetir: Hacer los pasos 2 a 4 hasta que se alcance la precisión deseada.

° Convergencia lineal: La convergencia es lineal, es decir, la cantidad de error se reduce a la mitad en cada iteración.

° Simplicidad: Es fácil de implementar y entender.

° No requiere derivadas: A diferencia de otros métodos, no necesita calcular derivadas.

° Resolución de ecuaciones: Utilizado para encontrar raíces de polinomios y funciones no lineales.

° Modelos económicos: Para encontrar equilibrios en modelos matemáticos de oferta y demanda.

° Algoritmos de optimización: En algoritmos que requieren encontrar puntos críticos de funciones.

° Problemas de física aplicada: Como el cálculo de trayectorias y fuerzas en sistemas mecánicos.