Método simplex.
Consiste en un algoritmo o método algebraico sistemático y eficiente para resolver problemas de programación lineal con dos o mas variables de decisión.
Problema Original Sin Variables De Holgura
Maximizar Z=5x1+6x2
Sujeto a:
x1 + x2 ≤ 80 Departamento de corte
3x1 +2x2 ≤ 220 Departamento de armado
3x1 + 3x2 ≤ 210 Departamento de acabado
x1 + x2 ≥ 0
Conceptos Básicos Del Método Simplex
Variable De Holgura
Es una variable No negativa que se suma al lado izquierdo de una restricción menor o igual, para obtener una restricción de igualdad.
Maximizar Z=5x1+6x2+0h2+0h3+0h3
Sujeto a:
x1+x2+h1+0h2+0h3=80
3x1+2x2+0h1+h2+0h3=220
2x1+3x2+0h1+0h2+h3=210
x1≥0, x2≥0,h1≥0,h2≥0,h3≥0
h1: Número de horas no utilizadas en el departamento de corte
h2: número de horas no utilizadas en el departamento de armado
h3: Número de horas no utilizadas en el departamento de acabado
h1,h2,h3, son variables de holgura no negativas
Variables Básicas y soluciones Básicas
En un problema de programación lineal con n variables (incluyendo las de holgura), y m ecuaciones, para hallar una solución básica, se igualan a cero n-m variables, las cuales se denominan no básicas, y las restantes se denominan variables básicas.
Solución Básica Factible
Una solución básica es factible cuando todas las variables toman valores no negativos.
Solución Básica No Factible
Una solución básica es no factible cuando una o algunas de sus variables toman valores negativos.
Variables No Básicas
Es un conjunto de variables de un problema de programación lineal, en forma estándar, cuyos valores se forman como cero.
x1=0, x2=0
Variables Básicas
Es una variable diferente de cero de un problema de programación lineal en forma estándar.
h1=80, h2=220,h3=210
método gráfico
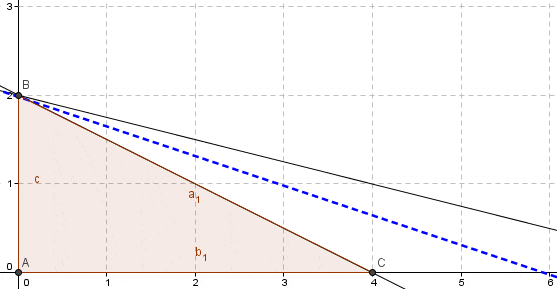
Por Solución múltiple
Se establece cuando al trasladar la recta Z no toca un solo punto extremo del área factible de solución; si no que por el contrario toca un segmento de la recta. cualquier combinación de producción sobre ese segmento de recta, sera solución óptima para el problema.
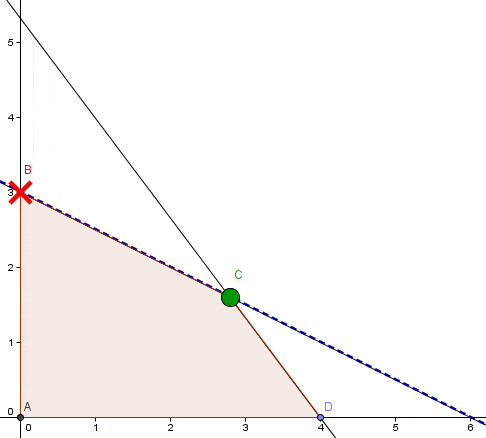
Por Solución No Acotada
En este tipo de problemas la solución se presenta en el infinito; ya que por más que uno traslade la recta Z paralelamente para buscar el punto más lejano del área factible de solución, nunca llegará.
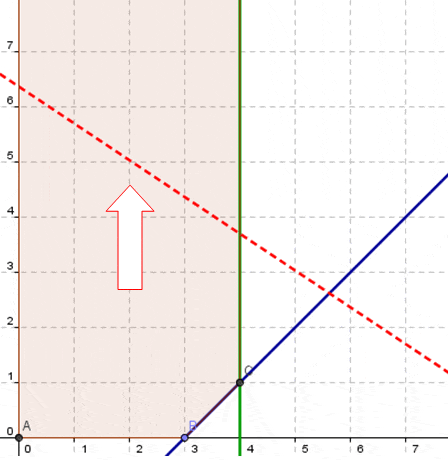
problemas sin solución
Un problema no tiene solución cuando no tiene área factible de solución; esto es que no hay un solo punto que satisfaga la totalidad de las restricciones del problema. para que un problema tenga solución debe tener por lo menos un punto común en todas las restricciones.
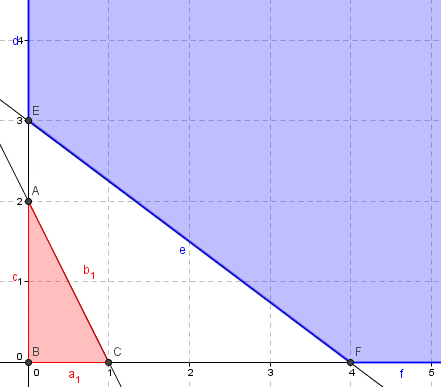
Solución Degenerada
Un problema de programación lineal genera solución básica factible degenerada cuando dentro del mismo hay restricciones de carácter redundante; es decir, hay más de una restricción que genera la misma área factible, por lo tanto la solución no varia si se elimina una de estas restricciones (si hay más de dos restricciones que generan la misma área factible, se pueden eliminar todas menos una y la solución no cambiará).