Quadratic Functions

y=a(x-h)^2+k

tells us what the graph
will look like.

VERTEX:
(h,k)

'h' is the x value of the vertex

'h' represents a
horizontal shift

'k' is the y value of the vertex

'k' represents a
vertical shift.

y=ax^2

y=a^2+bx+c

'a' = Vertical Stretch/
Compression Factor

Direction of Opening:

if a<0, the parabola opens
down. If a>0, the parabola
opens up.

If 'a' is a fraction/decimal
there is a vertical compression

If 'a' is greater then 1
there is a vertical stretch.

Step Patterns
___________
1, 3, 5

Multiply this step pattern
with 'a' Value to obtain the
correct points of a given parabola

'a' = 3

Step Pattern:
= 3 (1,3,5...)

New Step Pattern: 3, 9, 15....

To determine whether a relationship
is quadratic or linear.

Second Differences of a
quadratic function are
constant.

The Second differences in the
equation "y=2x^2-3x+1" are
constant.

This relationship is quadratic

a, b, and c are real numbers.

a ≠ 0.

'x' is the unknown
variable

'c' is the value of the
y-intercept of the
parabola.

Axis of Symmetry

x= -b/2a

y=a(x-r)(x-s)

Axis of Symmetry
(x-value of vertex)

r + s /2

y=(x-6)(x+2)
____________
r = 6 s = -2
____________
x vertex = r+s/2
= 6+(-2)/2
= 2
∴ the AOS is x=2

The A.O.S into factored
form equation to find

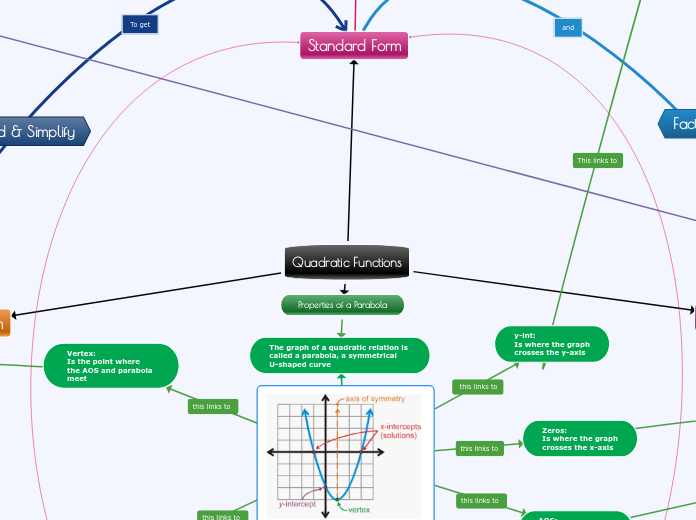
Properties of a Parabola

The graph of a quadratic relation is
called a parabola, a symmetrical
U-shaped curve

looking for a common multiple
so that the brackets can be put
into place.

Simple trinomials

2 numbers to add to
the middle term, & multiply to
the end term

x^2+bx+c
x^2+9x+14

Add: 7+2 = 9
Multiply: 7 x 2 + 14

Factored form: = (x+7) (x+2)

1. ALWAYS check for a GCF first!

2. To factor a simple trinomial of
x^2+bx+c, find 2 numbers that multiply to give c, & add to give b

3. use these to numbers, and write in factored form { y= a(x+r)(x+s). If there was a GCF, put it outside the first bracket.

Complex Trinomials

Decomposition: a process
used to factor complex trinomials

It means to break up the x term, and find 2
numbers whose product is 'ac' and sum is b

ax^2+bx+c
3x^2+14x+8

ac= (3)(8) = 24

Product: 24 Sum: 14

try 12 x 2 = 24 try 12 + 2 = 14

= 3x^2 + 12x + 2x + 8
= 3x (x+4) +2 (x+4)
= (3x+2) (x+4)

1. Multiply a & c together, and find 2 numbers that multiply to get 'ac' & add to get 'b'.

2. Rewrite the expression by decomposing the middle term with the numbers found in step 1

3. Continue with factoring by group/common factor.

By Grouping

to group terms
which have a common factor

= xy + 4x + 3y + 12
= x (y+4) + 3 (y +4)
= (y+4) (x+3)

1. divide the polynomials into
two groups

2. factor the GCF out of the 1st half
& factor the GCF out of the 2nd half

3. Next you should have a
common binomial

4. Factor out the common binomial

Perfect square Trinomials

you go from...
a^2 + 2ab +b^2 → (a+b)^2

OR

a^2 - 2ab + b^2 → (a-b)^2

=9x^2 + 12x + 4
= (3x + 2)^2

1. Sqaure root the values of a & b
in the standard form equation

2. use '2ab', and plug in the
'a' & 'b' values found in the first step, and
plug it into the expression 2ab to see whether it gives you the middle term. If it does multiply to the middle term, your equation is a perfect square trinomial.

Plug in the values of 'a' & 'b'
found in step 1, into (a+b)^2 OR (a-b)^2

used to turn Quadratic in Std.form
into factored form

Binomial Common Factors

if there are two binomials that are exactly
the same, think of the binomial as one factor.

= 4x(w+1) + 5y (w+1)
= (w+1)(4x+5y)

a^2+bx+c

By completing the square

the x intercepts

x^2+8x+4, plug in the 'a' 'b' & 'c' values
into the quadratic formula & solve to find the x-intercepts

HOW many x intercepts a quadratic equation has

DISCRIMINANTS: b^2-4ac

D>0: there are 2 solutions

D=0: there is 1 solution

D < 0: there are no solutions

Multiplying to
remove brackets

Use the FOIL Method
First, outside, inside, last

(3x+5)(2x+1)
= 6x^2+3x+10x+5
= 6x^2+13x+5

Binomials

(a+b)(c+d)
= ac+ad+bc+bd

Perfect Squares

a binomial is squared,
you multiply it by itself.

Adding a sqaured binomial

(a+b)^2

a^2+2ab+b^2

(3x+4)^2
= (3x+4) (3x+4)
= 9x^2+12x+12x+16
= 9x^2+24x+16

Subtracting a squared binomial

(a-b)^2

a^2-2ab+b^2

(x-5)^2
= (x-5)(x-5)
= x^2-5x-5x+25
=x^2-10x+25

Difference of
Squares

(a+b)(a-b)

a^2-b^2

(x+3)(x-3)
= x^2-3x+3x-9
=x^2-9
The middle terms cancel each
other out.

2 binomials have opposite signs
2 terms will cancel each other out.

The method of completing the square
can be used to express a quadratic relation

y=ax^2+bx+c

Vertex Form:
y=a(x-h)^2+k

y= -7x^2+14x-13

y= -7(x^2-2x)-3
(b/2)^2 = (2/2)^2 = 1

y= -7(x^2-2x+1-1)-3
y= -7(x^2-2x+1)7-3
y= -7(x^2-2x+1)+4

1. Put brackets around ax^2+bx

2. Make sure the 'a' value is 1 by
dividing only the 2 terms in the bracket with the a value, and then put the 'a' value
outside the bracket

3. Use the formula (b/2)^2,
and add, and SUBTRACT this value in the
brackets

4. multiply the subtracted value with the 'a'
value, and bring this number outside the bracket to add with the k value

5. Keep the 'a' value outside
the bracket & sqaure root the 1st term, keep only the SIGN of the middle term, & square root the third term in the bracket. Finally add a square sign outside the bracket.

6. Write out the final equation

VERTEX:
(Axis of Symmetry, Optimal Value)
(x,y)

The Optimal value for the equation
y=(x-6)(x+2) is...
y=(2-6)(2+2)
y=(-4)(4)
y=-16
∴ the Optimal Value is y=-16

AOS:
Divides parabola
into 2 equal halves

Vertex:
Is the point where
the AOS and parabola
meet

Zeros:
Is where the graph
crosses the x-axis

y-int:
Is where the graph
crosses the y-axis

Optimal Value:
Value of the
y-coordinate of the
vertex

Max/Min:
Determines whether
parabola opens
down or up

Optimal Value
(Y-Values of vertex)

Difference of Sqaures

two terms are being subtracted
a^ - b^2 → (a+b) (a-b)

=4x^2 - 9
= (2x-3)(2x+3)
Because 4 & 9 are perfect squares & this expression is finding the difference between the two terms, we have a difference of squares

1. square root the 'a' value &
'b' value.

2. once you have your a & b values,
plug those values into the expression
(a+b) (a-b)

'r' & 's' represent the
ZEROS of the parabola
or the X-INTERCEPTS.