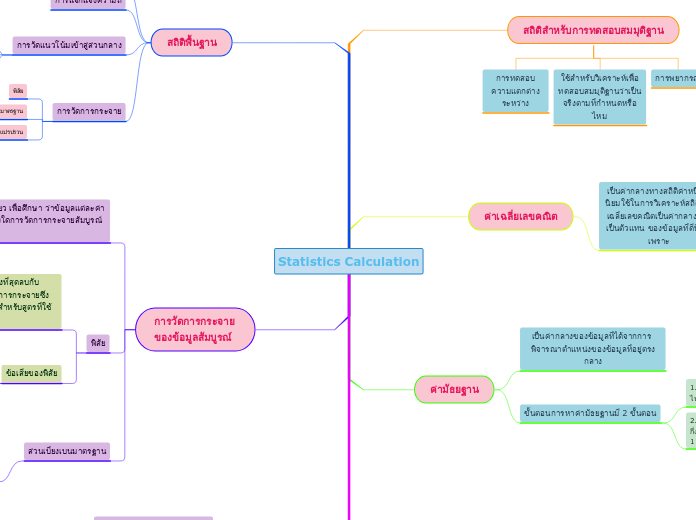
Statistics Calculation

การทดสอบความแตกต่างระหว่าง

ใช้สำหรับวิเคราะห์เพื่อทดสอบสมมุติฐานว่าเป็นจริงตามที่กำหนดหรือไหม

การพยากรณ์

เป็นค่ากลางทางสถิติค่าหนึ่ง ที่นิยมใช้ในการวิเคราะห์สถิติ ค่าเฉลี่ยเลขคณิตเป็นค่ากลางหรือเป็นตัวแทน ของข้อมูลที่ดีที่สุด เพราะ

1. เป็นค่าที่ไม่เอนเอียง

2. เป็นค่าที่มีความคงเส้นคงวา

3. เป็นค่าที่มีความแปรปรวนต่ำที่สุด

4. เป็นค่าที่มีประสิทธิภาพสูงสุด

เป็นค่ากลางของข้อมูลที่ได้จากการ พิจารณาตำแหน่งของข้อมูลที่อยู่ตรงกลาง

ขั้นตอนการหาค่ามัธยฐานมี 2 ขั้นตอน

1. เรียงลำดับข้อมูลจากมากไปน้อย หรือจากน้อยไปมาก

2. ทำการหาตำแหน่งกึ่งกลางที่ได้จากขั้นตอนที่ 1

แสดงความหมายของข้อมูลและใช้เป็นพื้นฐานในการคำนวณสถิติชั้นสูง

การแจกแจงความถี่

การวัดแนวโน้มเข้าสู่ส่วนกลาง

ค่าเฉลี่ย

มัธยฐาน

ฐานนิยม

การวัดการกระจาย

พิสัย

ความเบี่ยงเบนมาตรฐาน

ความแปรปรวน

การวัดการกระจายของข้อมูลเดียว เพื่อศึกษา ว่าข้อมูลแต่ละค่ามีความแตกต่างกันมากน้อยเพียงใดการวัดการกระจายสัมบูรณ์มี 4 วิธี

พิสัย

ส่วนเบี่ยงเบนควอร์ไทล์

ส่วนเบี่ยงเบนเฉลี่ย

ส่วนเบี่ยงเบนมาตรฐาน

พิสัย

การหาการกระจายของข้อมูลโดยนำข้อมูลที่สูงที่สุดลบกับข้อมูลที่มีค่าต่ำที่สุดเพื่อให้ได้ค่าที่เป็นช่วงของการกระจายซึ่งสามารถบอกถึงความกว้างของข้อมูลชุดนั้นๆ สำหรับสูตรที่ใช้ในการหาพิสัย คือ

ข้อเสียของพิสัย

1.ในกรณีที่ใช้พิสัยกับข้อมูลที่มีจำนวนมาก การวัดจะไม่แน่นอน

2. ค่าของพิสัยจะขึ้นอยู่กับขนาดของข้อมูลถ้าข้อมูลมีจำนวนมากพิสัยจะมากถ้าข้อมูลมีจำนวนน้อยพิสัยจะน้อย

ส่วนเบี่ยงเบนมาตรฐาน

เป็นค่าวัดการกระจายที่สำคัญทางสถิติ เพราะ เป็นค่าที่ใช้บอกถึง
การกระจายของข้อมูลได้ดีกว่าค่าพิสัย และ ค่าเฉลี่ยส่วนเบี่ยงเบน
มาตรฐาน(SD) ในกรณีข้อมูลไม่มีการแจกแจงความถี่

เป็นค่ากลางซึ่งนำมาใช้ในกรณี ที่ข้อมูลมีการซ้ำกันมากๆ จนผิดปกติ

เป็นค่ากลางหรือตัวแทนของข้อมูลที่สามารถ อธิบายลักษณะที่เกิดขึ้นได้ดีกว่า ค่าเฉลี่ยเลขคณิต และค่ามัธยฐาน

สามารถใช้ได้กับข้อมูลที่เป็นข้อมูลเชิงคุณภาพ ( Qualitative) และข้อมูลเชิงปริมาณ (Quantitative)