af BHJMG BHJMG 11 måneder siden
149
Señales continuas y discretas
af BHJMG BHJMG 11 måneder siden
149

Mere som dette
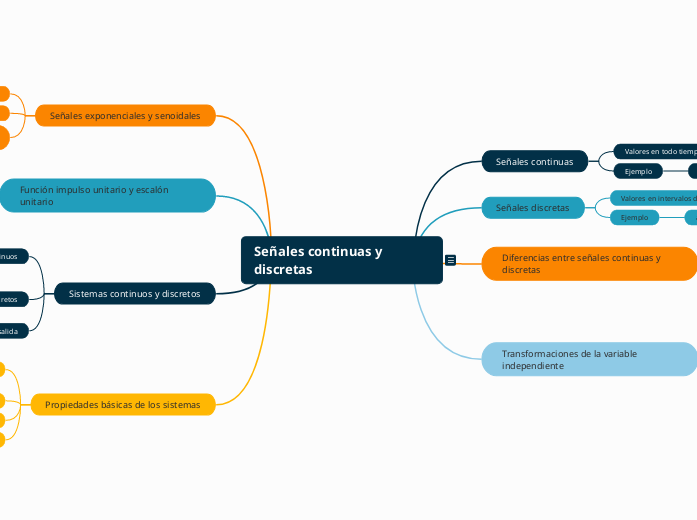
Señales continuas y discretas Señales continuas: Valores en todo tiempo continuo ( 𝑡 t). Ejemplo: corriente eléctrica. Señales discretas: Valores en intervalos de tiempo ( 𝑛 n). Ejemplo: audio digital. Diferencias: Representación en el tiempo, almacenamiento y procesamiento. Transformaciones de la variable independiente Desplazamiento en el tiempo: Adelanto ( 𝑥 ( 𝑡 − 𝑡 0 ) x(t−t 0 )), retraso ( 𝑥 ( 𝑡 + 𝑡 0 ) x(t+t 0 )). Escalado en el tiempo: Expansión ( 𝑥 ( 𝑎 𝑡 ) x(at)), compresión ( 𝑥 ( 𝑡 / 𝑎 ) x(t/a)). Reflejo: Inversión en el tiempo ( 𝑥 ( − 𝑡 ) x(−t)). Señales exponenciales y senoidales Exponenciales: 𝑥 ( 𝑡 ) = 𝐴 𝑒 𝜎 𝑡 x(t)=Ae σt , usadas en análisis de sistemas. Senoidales: 𝑥 ( 𝑡 ) = 𝐴 sin ( 𝜔 𝑡 + 𝜙 ) x(t)=Asin(ωt+ϕ), base para señales periódicas. Representación en el dominio del tiempo y frecuencia. Función impulso unitario y escalón unitario Impulso unitario ( 𝛿 ( 𝑡 ) δ(t)): Modelo ideal para representar eventos instantáneos. Escalón unitario ( 𝑢 ( 𝑡 ) u(t)): Representa cambios bruscos, como encendido o apagado. Relación: Derivada del escalón = impulso unitario. Sistemas continuos y discretos Continuos: Modelados por ecuaciones diferenciales, tiempo continuo. Discretos: Modelados por ecuaciones en diferencias, tiempo discreto. Relación entrada-salida: Respuesta impulsiva y convolución. Propiedades básicas de los sistemas Linealidad: Superposición y escalabilidad. Estabilidad: Respuesta acotada para entradas acotadas. Causalidad: Respuesta depende del presente o pasado, no del futuro. Invariancia en el tiempo: No cambia con desplazamientos en el tiempo.
no del futuro