von Basilis Kranias Vor 7 Jahren
763
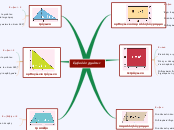
Εννοιολογικός χάρτης - Κοτζαμάνογλου
Εμβαδά επιπέδων σχημάτων και ιδιότητες.
von Basilis Kranias Vor 7 Jahren
763

Mehr dazu