von Ashlee Hernandez vor 18 Tagen
31
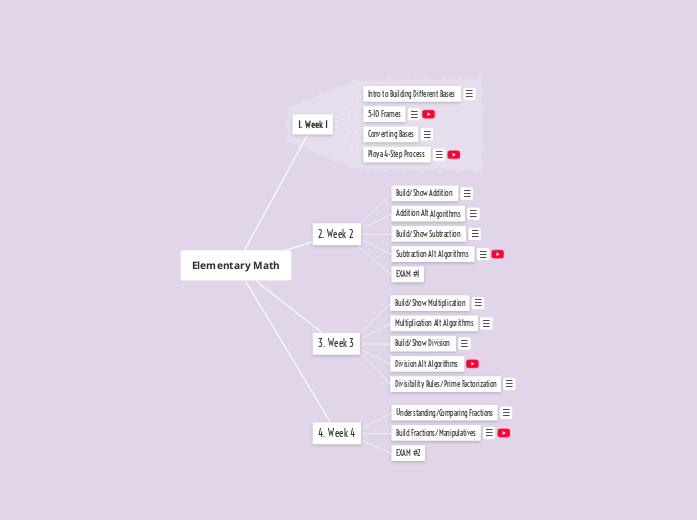
Elementary Math
von Ashlee Hernandez vor 18 Tagen
31

Organize your paragraphs using this mind map. It will help you map out all details related to a topic, so that you can organize them in coherent sentences.
In a fraction:
If the denominators are the same, just compare the numerators.
Example:
3/8 vs. 5/8 → 5/8 is greater (because 5 pieces is more than 3 when the size is the same)
If the numerators are the same, the fraction with the smaller denominator is greater (because the pieces are bigger).
Example:
3/5 vs. 3/8 → 3/5 is greater (because fifths are bigger than eighths)
Look at how many pieces are missing to reach the whole amount.
Example:
5/6 is missing 1 piece (1/6)
7/8 is missing 1 piece (1/8)
Since 1/8 is smaller than 1/6, 7/8 is closer to 1 → 7/8 is greater
2 – Number ends in 0, 2, 4, 6, or 8
3 – Sum of the digits is divisible by 3
4 – Last 2 digits are divisible by 4
5 – Number ends in 0 or 5
6 – Number is divisible by both 2 and 3
9 – Sum of the digits is divisible by 9
10 – Number ends in 0
Example:
36
→ 6 × 6
→ 2 × 3 and 2 × 3
Prime factors: 2 × 2 × 3 × 3
Step 1: Build the Total Using Units
Start with the number you're dividing (the dividend) and represent it using individual units.
Step 2: Make Equal Groups
Group the units based on the divisor. Keep grouping until you can't make a full group anymore.
Step 3: Count the Groups
The number of full groups is your whole-number answer.
Step 4: Leftover Units Become a Fraction
If some units are left over, write them as a fraction over the divisor.
8 ÷ 3
63 ÷ 12
Why this helps:
Break apart the number using place value, then multiply each part.
Example: 23 × 4
→ 23 = 20 + 3
→ (20 × 4) + (3 × 4)
→ 80 + 12 = 92
Why it helps:
Multiply the biggest place value first, then move to the right.
Example: 23 × 4
→ 20 × 4 = 80
→ 3 × 4 = 12
→ 80 + 12 = 92
Why it helps:
In this strategy, each number is broken into its place value parts (tens and ones). You draw a box or grid and label the top and sides with those parts. Then, you multiply each pair of numbers and write the answers in each section of the box. Finally, you add all the partial products together to get the total.
Why it helps:
This strategy uses a grid to organize the multiplication of each digit. You draw a box divided into diagonals and label the digits of the numbers on the top and sides. Each box shows one multiplication, with tens written in the top triangle and ones in the bottom. After all parts are filled in, you add diagonally and combine the sums to get the final answer.
Why it helps:
This shows multiplication as a certain number of groups with the same number in each group.
Example: 3 × 4
Visual:
Circle 1 → ⚫⚫⚫⚫
Circle 2 → ⚫⚫⚫⚫
Circle 3 → ⚫⚫⚫⚫
Then count all the dots: 4 + 4 + 4 = 12
Why this helps:
This uses rows and columns to represent multiplication.
Example: 3 × 4
Visual:
⚫ ⚫ ⚫ ⚫
⚫ ⚫ ⚫ ⚫
⚫ ⚫ ⚫ ⚫
Count all: 3 rows × 4 columns = 12
Why this helps:
This method uses place value to break apart numbers and multiply them in parts.
Example: 13 × 14
Step 1: Break each number into tens and ones
13 = 10 + 3
14 = 10 + 4
Step 2: Set up the box with one number on the top and one on the side:
10 | 3
------------------
10| 100 | 30
4 | 40 | 12
Step 3: Multiply each part
Step 4: Add all the pieces together
100 + 30 + 40 + 12 = 182
Break both numbers into tens and ones, then subtract each part.
Example:
74 – 52
→ 70 + 4 and 50 + 2
→ 70 – 50 = 20
→ 4 – 2 = 2
→ 20 + 2 = 22
Why it helps:
It shows exactly how much is being taken away from each place value.
Start with the biggest place value and move left to right.
Example:
74 – 52
→ 70 – 50 = 20
→ 4 – 2 = 2
→ 20 + 2 = 22
Why it helps:
It matches how we read numbers and builds mental math confidence.
Change both numbers by the same amount to make subtraction easier.
Example:
74 – 49
→ Add 1 to both numbers: 75 – 50
→ 75 – 50 = 25
Why it helps:
It keeps the difference the same while making the math easier to do in your head.
How to Show Subtraction with Base Ten Blocks
We use base ten blocks (longs and units) to help students see what subtraction really means, taking away, regrouping, and comparing amounts.
Base Ten Blocks You’ll Use:
Steps to Build and Subtract:
Step 1: Build the First Number
Use base ten blocks to build the number you're starting with.
Example: 42 – 18
Step 2: Subtract What You Can
Try to subtract the units (ones) and longs (tens) from what you built.
In this example:
Now you have:
Step 3: Regroup if Needed
Regroup when there aren’t enough units to subtract.
Now subtract:
Step 4: Count What’s Left
You’re done once you’ve subtracted everything.
Why This Helps:
Break each number into tens and ones, then add those parts.
Example:
47 + 36
→ 40 + 7 + 30 + 6
→ (40 + 30) + (7 + 6)
→ 70 + 13 = 83
Why it helps:
It reinforces place value and shows where each part of the sum comes from.
Start by adding the biggest place values first (usually tens), then move right.
Example:
47 + 36
→ 40 + 30 = 70
→ 7 + 6 = 13
→ 70 + 13 = 83
Why it helps:
It’s how we usually read numbers and build mental math skills.
Change one number to a “friendly” number (like a multiple of 10), then adjust.
Example:
47 + 36
→ Think: 47 + 3 = 50 (add 3 to make a friendly number)
→ Then: 36 - 3 = 33
→ Now: 50 + 33 = 83
Why it helps:
It makes numbers easier to work with mentally, especially for rounding or regrouping.
Add to one number and subtract from the other so the total stays the same.
Example:
47 + 36
→ Add 3 to 47 (now it’s 50)
→ Subtract 3 from 36 (now it’s 33)
→ 50 + 33 = 83
Why it helps:
It teaches balance in math and is great for quick mental calculations.
Let’s say you have 24 in base five (24₅). That means:
Another number, 13₅, would be:
Put all the longs and units together:
After regrouping, count how many longs and units you have left.
Write the new number in the same base you started with.
24₅ + 13₅
Polya’s 4-Step Problem-Solving Process
24 ----> l l ....
24 to base six ---> ll ....
Converting to Base 10
14 base five ---> l .... 5+4=9
26 to base 12 ---> ll ....... 12+12+6=30
*Base states the number of units in each shape.
A 5-frame is a row of 5 boxes used in math to:
A ten-frame is a row of 10 boxes used in math to:
80 base 5 to base 10
llllllll =40