によって Dennise Maricela Zambrano Meza 4年前.
3229
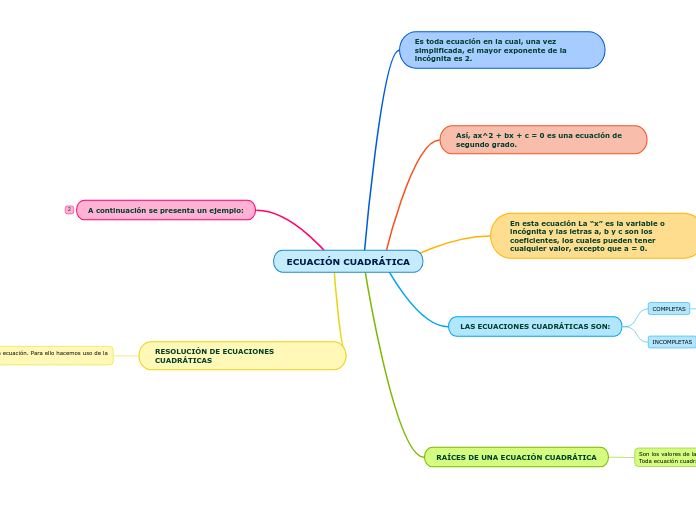
ECUACIÓN CUADRÁTICA
によって Dennise Maricela Zambrano Meza 4年前.
3229

もっと見る
* Si es positivo, hay DOS soluciones * Si es cero sólo hay UNA solución, * y si es negativo hay dos soluciones que incluyen números imaginarios.