によって Wafiqah Wahab 5年前.
494
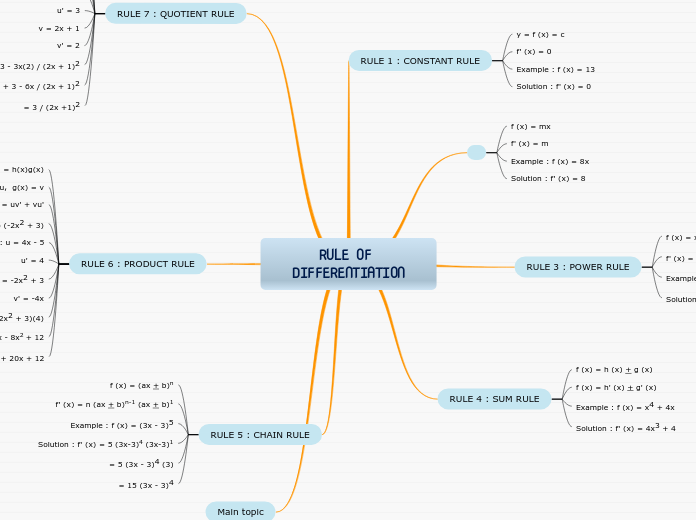
RULE OF DIFFERENTIATION
によって Wafiqah Wahab 5年前.
494

もっと見る

Jawdat Laveezaにより

Amanda Trehearnにより

John Kelabuにより

Esmeralda Nohemí Pérez Garcíaにより