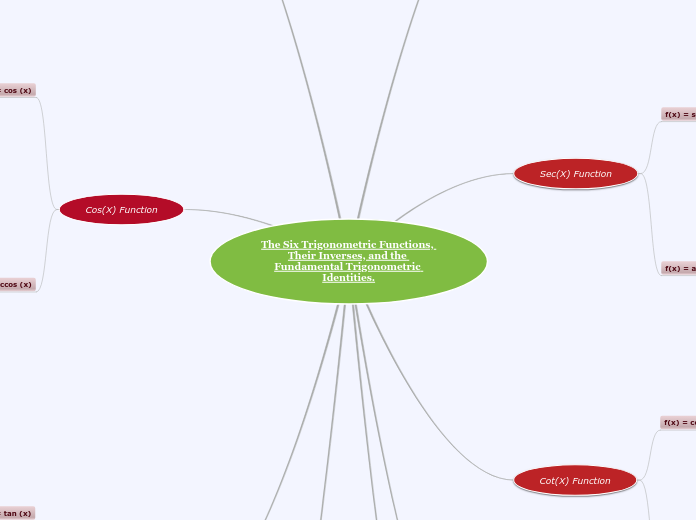
A Must Know in Trigonometry

Cell nucleus

by Felipe Miranda

Fun Ways to Learn

by Jef Fisher

iBatis Data Mapper 2.0

by aakarsh nair

Unit 1 - Functions: Characteristics and Properties

by Grishma Bk

The Six Trigonometric Functions, Their Inverses, and the Fundamental Trigonometric Identities.

Quotient identities

COT (X) = Cos(X)/Sin(X)

TAN (X) = Sin(X)/Cos(X)

Tan(X) Function

f(x) = arctan (x)

Range: (−π/2,π/2)

f(x) = tan (x)

Range: all real numbers

Domain: all real numbers except pi/2 + k pi, k is an integer.

Cos(X) Function

f(x) = arccos (x)

Range: [0,π]

f(x) = cos (x)

Range: [-1 , 1]

Sin(X) Function

f(x) = arcsin (x)

Range: [−π/2,π/2]

Domain: [−1,1]

f(x) = sin (x)

Period = 2pi

Range: [-1 , 1]

Domain: all real numbers

Subtopic

Pythagorean Identities

1 + Cot^2(X) = CSC(x)

1 + Tan^2(x) = Sec^2(X)

Sin^2(x) + Cos^2(x) = 1

Reciprocal identities

COT (X) = 1/ TAN (X)

SEC (X) = 1/ COS (x)

CSC (X) = 1/ SIN (X)

TAN (x) = 1/ COT (X)

COS (X) = 1 /SEC (X)

SIN (X) = 1/CSC (X)

Cot(X) Function

f(x) = arccot (x)

Astmtote: y=pi/4; 17pi/4

Range: (0,π)

Domain: (−∞,∞)

f(x) = cot (x)

Period = pi

Range: all real numbers

Domain: all real numbers except k pi, k is an integer

Sec(X) Function

f(x) = arcsec (x)

Asymptote: y = -pi

Range: [0,π/2)∪(π/2,π]

f(x) = sec (x)

Vertical asymptotes: x = pi/2 + k pi, where k is an integer.

Period = 2 pi

Range: (-infinity , -1] U [1 , +infinity)

Domain: all real numbers except pi/2 + k pi, n is an integer

Csc(X) Function

f(x) = arccsc (x)

Asymtote: y= -pi

Range: [−π/2,0)∪(0,π/2]

Domain: (−∞,−1]∪[1,∞)

f(x) = csc (x)

Properties

Vertical asymptotes: x = k pi, where k is an integer.