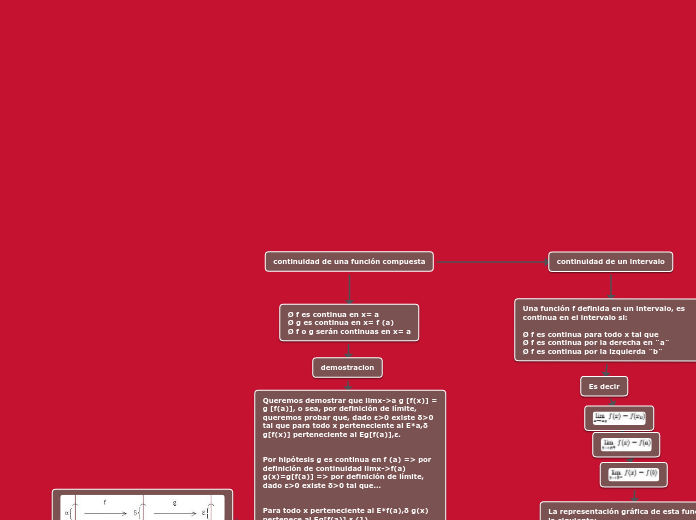
continuidad de una función compuesta

Więcej takich

Bronislaw Malinowsky

przez Yolima ramirez

Organigrama

przez María Parco

Sample Mind Map

przez Sandra Mandujano

Modelos de Optimización

przez Carolina Solano Franco

continuidad de una función compuesta

continuidad de un intervalo

Una función f definida en un intervalo, es continua en el intervalo si: Ø f es continua para todo x tal que Ø f es continua por la derecha en ¨a¨ Ø f es continua por la izquierda ¨b¨

Es decir

La representación gráfica de esta función es la siguiente: También se tiene que una función definida en el intervalo , es continua en ese intervalo, si y solo si es continua en el intervalo abierto y es continua por la derecha de "a". Similarmente, para que una función definida en el intervalo sea continua en ese intervalo, es necesario que sea continua en el intervalo abierto y a la vez que sea continua por la izquierda en "b".

Continuidad en un intervalo abierto: Una función f es continua en un intervalo abierto (a,b) si lo es en todo número del intervalo. Continuidad en un intervalo por la izquierda: Una función f es continua por la izquierda en el punto x = x1 si el límite lateral por la izquierda y el valor de la función en el punto son iguales. Continuidad en un intervalo por la derecha:Una función f es continua por la derecha en el punto x = x1 si su límite lateral por la derecha y el valor de la función en el punto son iguales.

Ø f es continua en x= a Ø g es continua en x= f (a) Ø f o g serán continuas en x= a

demostracion

Queremos demostrar que limx->a g [f(x)] = g [f(a)], o sea, por definición de límite, queremos probar que, dado ε>0 existe δ>0 tal que para todo x perteneciente al E*a,δ g[f(x)] perteneciente al Eg[f(a)],ε. Por hipótesis g es continua en f (a) => por definición de continuidad limx->f(a) g(x)=g[f(a)] => por definición de límite, dado ε>0 existe δ>0 tal que... Para todo x perteneciente al E*f(a),δ g(x) pertenece al Eg[f(a)],ε (1) Por hipótesis f es continua en a tenemos por definición de continuidad limx->a f (x) = f (a), es decir que (por definición de límite) si tomamos el número δ de (1), existe α>0 tal que... Para todo x perteneciente al E*a,α f(x) pertenece al Ef(a),δ (2) De (1) y (2) se deduce que: Dado ε>0 existe α>0 / para todo x perteneciente al E*a,α g[f(x)] pertenece al Eg[f(a)],ε.