przez Christopher Voss 12 lat temu
479
Diff EQ
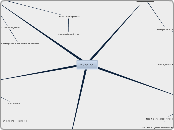
mapping out how to solve a differential equation based on certain parameters
przez Christopher Voss 12 lat temu
479

Więcej takich
tTake determinant, solve for lamda, plug in eigenvalue for general solution. If IVP plus in those values and solve for constants
variation of parameters
undetermined coefficients
repeated: y(t) = c1e^(r1t)+c2te^(r2t)
imaginary: y(t) = e^(at)(c1cosbt+c2sinbt)
real: y(h) = c1e^(r1t)+c2e^(r2t)