Equipo #3 - Mapa Mental

Więcej takich

RESPONSABILIDAD POR LA FUNCIÓN PÚBLICA

przez Carmen Reyes

Gobierno de Benito Juárez, 1867-1872 al gobierno de Sebastián Lerdo de Tejada, 1821-1876

przez Alejandro Guevara

mapa conceptual MICROSOFT OFFICE EXCEL Y MICROSOFT OFFICE ACCESS nicol castrillon 901

przez Nicol Sofia Castrillon 901

Modelo de Desarrollo Acelerado

przez Luis Fernando Reyes

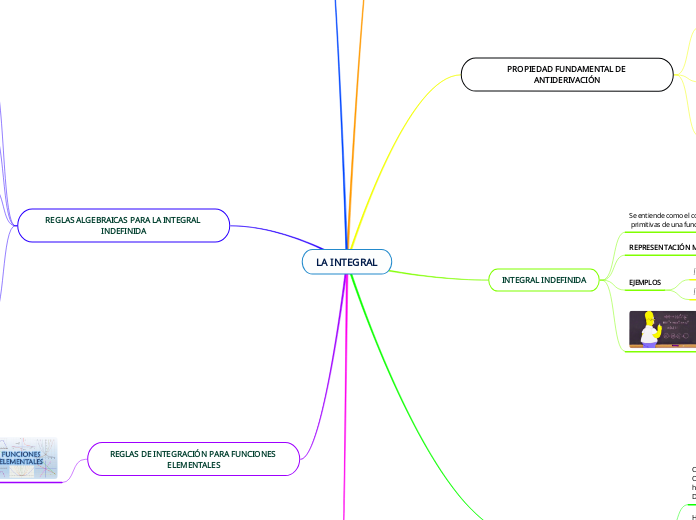
LA INTEGRAL

¿QUÉ ES?

"Se denomina antiderivada de una función f(x) a la función F(x)+C, donde C se constituye como una constante." (Pérez, J. 2021)

La integral o antiderivada se conoce por ser la operación inversa de derivar, así como la factorización es la operación inversa de la multiplicación.

∫ 6x*dx= 3x^2+C

Siendo x la variable y dx el indicador que dicha función derivó de esa incognita

∫ 5dx= 5x+C

REGLAS DE INTEGRACIÓN PARA FUNCIONES ELEMENTALES

REGLAS ALGEBRAICAS PARA LA INTEGRAL INDEFINIDA

∫( x^3+2x-7/x) dx = ∫(x^3/x + 2x/x - 7/x) dx = ∫ (x^2 + 2- 7/x) dx = ∫ x^2 dx + ∫ 2 dx - ∫ 7/x dx = 1/3 x^3 + 2x - 7 ln |x| + c

∫ (x^1/3 - 3x^-2/3 + 6) dx = ∫ x^1/3 dx - ∫ 3x^-2/3 dx + ∫ 6 dx = ∫ x^1/3 dx - 3 ∫ x^-2/3 dx + 6 ∫ dx = x^4/3/4/3 - 3. x^1/3 / 1/3 + 6x + c = 3x raíz cúbica x/ 4 - 9 raíz cúbica x + 6x + c

REGLA DEL FACTOR CONSTANTE

∫ k f(x)= k ∫ f(x) dx (cuando k es una constante)

Para integrar una función constante debemos sacar la constante de la integral de manera que multiplique a la integral de la función.

REGLA DE LA DIFERENCIA

∫ [f(x) - g(x)] dx= ∫ f(x) dx - ∫ g(x) dx

Para integrar una diferencia de funciones debemos separar y restar cada una de las integrales de las funciones

REGLA DE LA SUMA

∫ [f(x) + g(x)] dx= ∫ f(x) dx + ∫ g(x) dx

Para integrar una suma de funciones debemos separar y sumar cada una de las integrales de las funciones

APLICACIONES ECONÓMICAS PARA LA INTEGRAL INDEFINIDA

En la economía se utiliza la integral indefinida para calcular el costo, el ingreso y la utilidad totales por medio del costo, del ingreso y de la utilidad marginales.

Esto sirve para maximizar las operaciones y los beneficios de la empresa al conocer los máximos y mínimos de producción al encontrar los incrementos de los costos e ingresos cuando se realiza la producción y venta adicional de un bien. Estos datos ayudan a las empresas en la toma de decisiones.

Ejemplo costo total

Un fabricante estima que el costo marginal por producir ¨ q¨ unidades de cierto bien es C` (q) = 3q^2-24q+48 dólares por unidad. Si el costo de producción de 10 unidades es de 5000 dólares, ¿Cuál es la producción de 30 unidades?

Solución: C` (q)= 3q^2-24q+48 C(q)= ∫(3q^2-24q+48) dq = ∫3q^2 dq - ∫24q dq + ∫48 dq = 3∫q^2 dq - 24 ∫q dq + 48 ∫dq = 3q^3/3 - 24q^2/2 + 48q = q^3 - 12q^2 + 48q + c C(10)= 5000 = (10)^3 - 12(10)^2 + 48(10) + c 5000 - 1000 + 1200 - 480 = c c = 4720 C(30) = (30)^3 - 12(30)^2 + 48(30) + 4270 C(30)= 22360$

REFERENCIAS BIBLIOGRÁFICAS

Reyes Alva, E. (2018). Integrales Indefinidas. Universidad Nacional Toribio Rodríguez de Mendoza de Amazonas. Obtenido de: https://www.studocu.com/latam/document/universidad-nacional/calculo-ii/integrales-indefinidas-y-sus-aplicaciones/3943878

Hoffman, L., Bradley, G., Rosen, K. (2006). Cálculo Aplicado para Administración, economía y ciencias sociales. (8va edición). México: McGraw-Hill Interamericana.

Campus Virtual USAL (s.f.). Tema, 5 Integral Indefinida. Obtenido de: https://campus.usal.es/~mpg/Personales/PersonalMAGL/Docencia/TeoriaTema5CalculoCA11-12.pdf

INTEGRAL INDEFINIDA

EJEMPLOS

∫ (2/x) dx = 2Ln|x| + C

∫ -4dx = -4x + C

REPRESENTACIÓN MATEMÁTICA

∫ f(x)dx = F(x) + C

donde C es una constante.

Se entiende como el conjunto de todas las funciones primitivas de una función f(x) en un intervalo (a, b).

PROPIEDAD FUNDAMENTAL DE ANTIDERIVACIÓN

EJEMPLO

Demostrar que F(x) = x^4 + 4 y G(x) = x^4 + 10 son antiderivadas de H(x) = 4x^3

F´ (x) = 4x^3 = H(x) G´ (x) = 4x^3 = H(x)

CONCLUSIÓN

Ambas son antiderivadas de H(x), es decir F´´ (x) = G'(x) = H(x). Y se comprueba que y = F(x) = G(x) + C

INTERPRETACIÓN GEOMÉTRICA

La pendiente F´´ (x) de la recta tangente a y=F(x) en (x,F(x)) es la misma que la pendiente G´´ (x) de la recta tangente a y=G(x) en el punto (x,G(x)).

SIGNIFICA QUE

Son rectas paralelas, y ya que esta condición se cumple para toda x se concluye que la curva y=G(x) es paralela a la curva y=F(x).

y = G(x) = F(x) + C

DEFINICIÓN FORMAL

Si F(x) es una antiderivada de la función continua f(x), entonces cualquier otra antiderivada de f(x) tiene la forma G(x) = F(x) + C para alguna constante C.

EN POCAS PALABRAS

Si F y G son antiderivadas de R, entonces G´´ (x) = F'(x) = R(x).

Fecha: 21/01/2022 Universidad Metropolitana Equipo 3 Guenni, David; CI: 29.551.528; Carnet: 20211110358 Rencsar, Claudia; CI: 29.625.467; Carnet: 20211110871 Marquez, Rafael; CI: 27.692.907; Carnet: 20191110719 Soto, Sebastian ; CI: 28.547.265, Carnet: 20201110527 Salvuchi, Julio; CI:27.769.386, Carnet: 20201110122