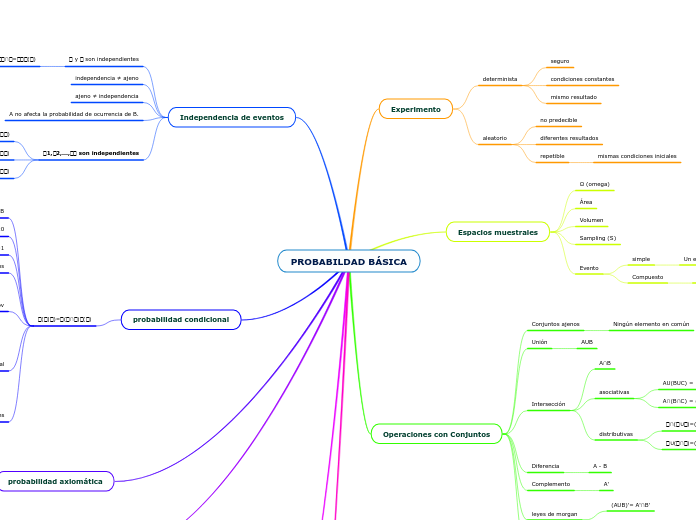
PROBABILDAD BÁSICA
probabilidad clásica
P(A)= #A / #S'
Ajenos
P(AUB) = P(A) + P(B)
S = Equiprobable
S = Finito
probabilidad geométrica
𝑃(𝐴)=Área de 𝐴 / Área de 𝑆
P(S) = 1
Real
P(A) ≥ 0
volumen
Ω es un subconjunto de R^3
longitud
Ω es un subconjunto de R
Ω es equiprobable
probabilidad frecuentista
𝑃(𝐴)=lim𝑛→∞ 𝑛𝐴 / 𝑛'
Aproximación empírica
𝑃(𝐴)≈𝑛𝐴 / 𝑛
No es exacto
subjetiva
probabilidad axiomática
axioma
Postulado válido
reglas de probabilidad
P(
𝑃(𝑆)=1
𝑃(𝐴)≥0
probabilidad condicional
𝑃(𝐴|𝐵)=𝑃(𝐴∩𝐵)𝑃(𝐵)
Teorema de Bayes
segunda probabilidad
probabilidad a posteriori
P(A1|B1)
probabilidad inicial
probabilidad a priori
Teorema de probabilidad total
partición finita de Ω
Un𝑖=1𝑛𝐵𝑖=𝑆
𝐵𝑖∩𝐵𝑗=∅para 𝑖≠𝑗
𝐵𝑖≠∅para 𝑖=1,...,𝑛
cumple los tres axiomas de Kolmogorov
P(A1UA2|B) = P(A1|B) + P(A2|B)
P(A|B)≥ 0
P(Ω|B)= 1
Si A y B son ajenos
El numerador es cero
𝑃(𝑆|𝐵)=1
𝑃(𝐴|𝐵)≥0
Probabilidad de A dado B
Independencia de eventos
𝐴1,𝐴2,...,𝐴𝑛 son independientes
𝑃(𝐴𝑖∩𝐴2∩⋯∩𝐴𝑛)=𝑃(𝐴1)𝑃(𝐴2)...𝑃(𝐴𝑛)
𝑃(𝐴𝑖∩𝐴𝑗∩𝐴𝑘)=𝑃(𝐴𝑖)𝑃(𝐴𝑗)𝑃(𝐴𝑘)
𝑃(𝐴𝑖∩𝐴𝑗)=𝑃(𝐴𝑖)𝑃(𝐴𝑗)
A no afecta la probabilidad de ocurrencia de B.
ajeno ≠ independencia
independencia ≠ ajeno
𝐴 y 𝐵 son independientes
𝑃𝐴∩𝐵=𝑃𝐴𝑃(𝐵)
Operaciones con Conjuntos
conjunto vacío (Ø)
leyes de morgan
( A∩B)'=A'UB'
(AUB)'= A'∩B'
Complemento
A'
Diferencia
A - B
Intersección
distributivas
𝐴∪(𝐵∩𝐶)=(𝐴∪𝐵)∩(𝐴∪𝐶)
𝐴∩(𝐵∪𝐶)=(𝐴∩𝐵)∪(𝐴∩𝐶)
asociativas
A∩(B∩C) = (A∩B)∩C
AU(BUC) = (AUB)UC
A∩B
Unión
AUB
Conjuntos ajenos
Ningún elemento en común
Espacios muestrales
Evento
Compuesto
Mas de un elemento de S
simple
Un elemento de S
Sampling (S)
Volumen
Área
Ω (omega)
Experimento
aleatorio
repetible
mismas condiciones iniciales
diferentes resultados
no predecible
determinista
mismo resultado
condiciones constantes
seguro