por Сюникаева Александра 6 anos atrás
609
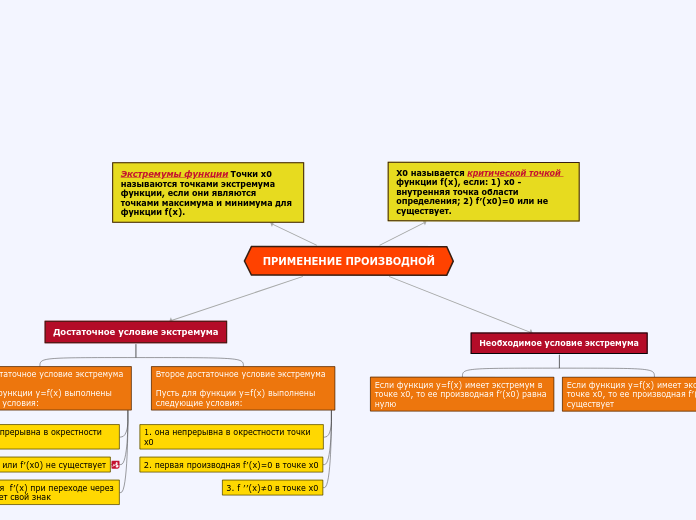
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
This is a sample mind map
por Сюникаева Александра 6 anos atrás
609

Mais informações