realizată de Allison Aguilar 6 ani în urmă
334
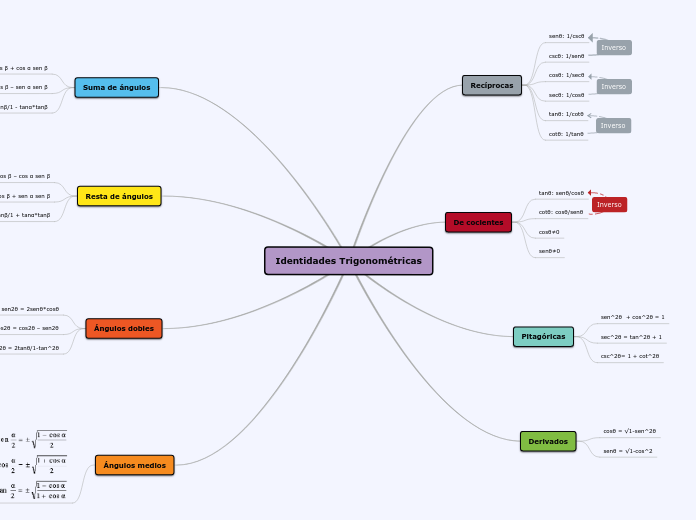
Identidades Trigonométricas
realizată de Allison Aguilar 6 ani în urmă
334

Mai multe ca acesta